Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O;R) tại M. Gọi H là hình chiếu của M lên đường thẳng OA. M thuộc mặt phẳng nào trong những mặt phẳng sau đây?A. Mặt phẳng qua H và vuông góc với OAB. Mặt phẳng trung trực của OAC. Mặt phẳng qua O và vuông góc với AMD. Mặt phẳng qua A và vuông góc với...
Đọc tiếp
Một đường thẳng d thay đổi qua A và tiếp xúc với mặt cầu S(O;R) tại M. Gọi H là hình chiếu của M lên đường thẳng OA. M thuộc mặt phẳng nào trong những mặt phẳng sau đây?
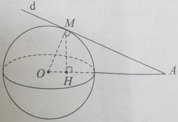
A. Mặt phẳng qua H và vuông góc với OA
B. Mặt phẳng trung trực của OA
C. Mặt phẳng qua O và vuông góc với AM
D. Mặt phẳng qua A và vuông góc với OM.

Chọn A.
Trong mặt phẳng (d,O), tam giác OMA vuông tại M có MH là đường cao nên:
⇒ H cố định
Vậy M thuộc mặt phẳng vuông góc với OA tại H.