Các cạnh của một tam giác có độ dài 4cm, 6cm và 6cm. Hãy tính góc nhỏ nhất của tam giác đó.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
18 tháng 7 2019
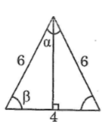
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có: cosβ=26=13⇒β≈70∘32′cosβ=26=13⇒β≈70∘32′
Suy ra: α=180∘–(β+β)=180∘–2.70∘32'=38∘56′α=180∘–(β+β)=180∘–2.70∘32′=38∘56′
Vậy góc nhỏ nhất của tam giác bằng 38∘56′38∘56′.
HQ
Hà Quang Minh
Giáo viên
14 tháng 9 2023
Vì tam giác \(ABC\) đồng dạng với tam giác \(A'B'C'\) nên tam giác \(A'B'C'\) đồng dạng với tam giác \(ABC\). Do đó, \(\frac{{A'B'}}{{AB}} = \frac{{B'C'}}{{BC}} = \frac{{A'C'}}{{AC}}\) (các cặp cạnh tương ứng có cùng tỉ lệ)
Thay số, \(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6}\). Áp dụng tính chất dãy tỉ số bằng nhau ta được:
\(\frac{{A'B'}}{4} = \frac{{B'C'}}{9} = \frac{{A'C'}}{6} = \frac{{A'B' + B'C' + A'C'}}{{4 + 6 + 9}} = \frac{{66,5}}{{19}} = 3,5\)
Ta có:
\(\left\{ \begin{array}{l}\frac{{A'B'}}{4} = 3,5 \Rightarrow A'B' = 3,5.4 = 14\\\frac{{A'C'}}{6} = 3,5 \Rightarrow A'C' = 3,5.6 = 21\\\frac{{B'C'}}{9} = 3,5 \Rightarrow B'C' = 3,5.9 = 31,5\end{array} \right.\)
Vậy \(A'B' = 14cm,A'C' = 21cm,B'C' = 31,5cm\).
11 tháng 11 2016
goị 3 cạnh của tam giác MNP là a,b,c
theo đề ta có : a/3=b/4=c/5 => c lớn nhất , a nhỏ nhất và c-a=6
Đặt a/3=b/4=c/5=k(k khác 0)
=> a=3k;b=4k;c=5k
=>c-a=5k-3k=6 =>2k=6 => k=3
<=>a=3.3=9 ; b=3.4=12 ; c=3.5=15
Vậy : độ dài các cạnh của tam giác lần lượt là 9 cm , 12cm,15cm
26 tháng 3 2016
a) Ta có 3 – 2 < 6 < 3 + 2
2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4
2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3
3cm, 4cm, 6cm là 3 cạnh của một tam giác.
TK NHA !!!
26 tháng 3 2016
a) Ta có 3 – 2 < 6 < 3 + 2 bất đẳng thức này sai nên ba độ dài 2cm, 3cm, 6cm không là ba cạnh của tam giác.
b) Vì 6 = 2 + 4 nên ba độ dài là 2cm, 4cm, 6cm không là 3 cạnh của một tam giác
c) 4 – 3 < 6 < 4 + 3 bất đẳng thức đúng nên ba độ dài 3cm, 4cm, 6cm là 3 cạnh của một tam giác.
K NHÉ!!!!!!!
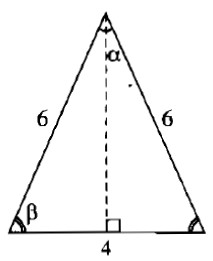
Vì các cạnh của tam giác lần lượt là 4cm, 6cm và 6cm nên tam giác đó là tam giác cân. Góc nhỏ nhất của tam giác là góc đối diện với cạnh 4cm.
Kẻ đường cao từ đỉnh của góc nhỏ nhất. Đường cao chia cạnh đáy thành hai phần bằng nhau mỗi phần 2cm.
Ta có:
cos β = 2/6 = 1/3 ⇒ β ≈ 70 ° 32 '
Suy ra: α = 180 ° - β + β = 180 ° - 2 . 70 ° 32 ' = 38 ° 56 '
Vậy góc nhỏ nhất của tam giác bằng 38 ° 56 '