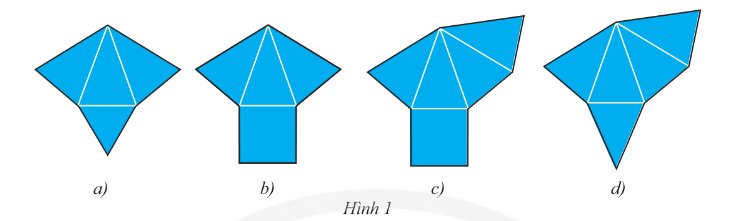
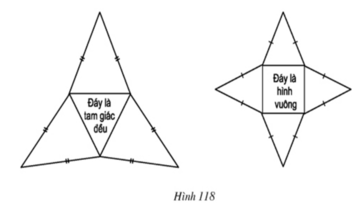
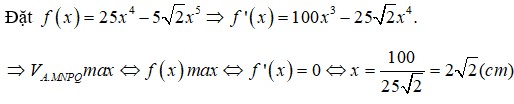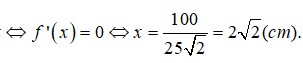Cắt từ tấm bìa cứng thành các hình như ở hình 118 rồi gấp lại để có những hình chóp đều.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


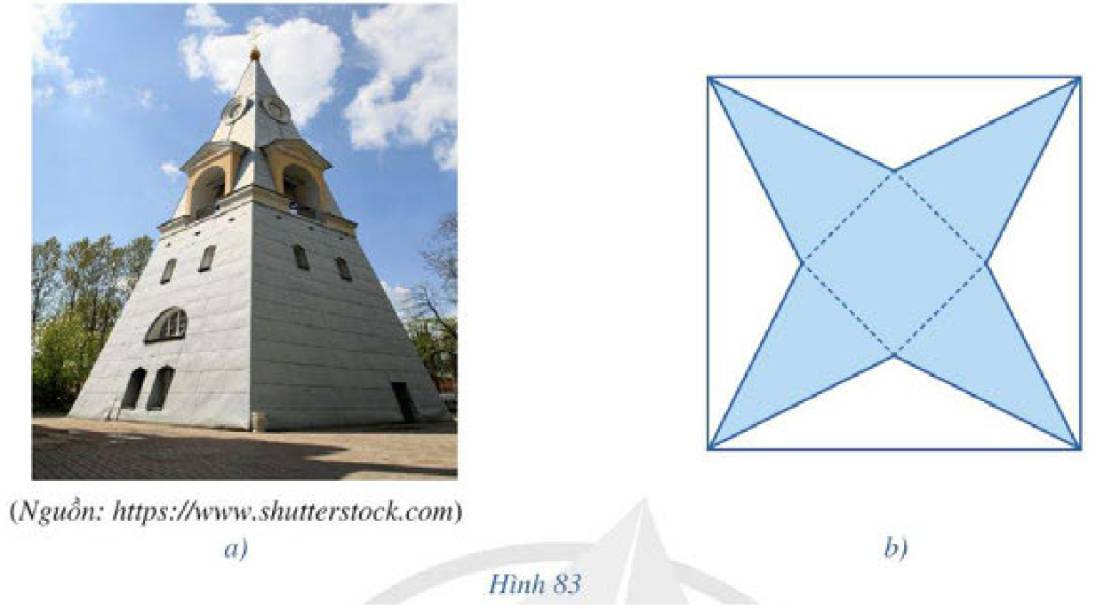
a: Tứ giác đó là hình vuông
b: Các cạnh bên của hình chóp đó bằng nhau

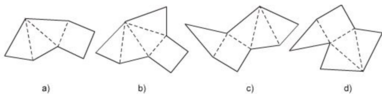
Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.

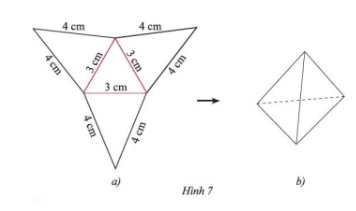
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.

Hình a, khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d, khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.

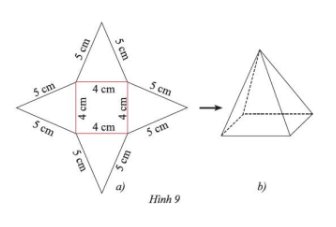
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.

1a gấp được thành hình chóp tam giác đều
1c gấp được thành hình chóp tứ giác đều

Đáp án C
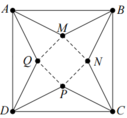
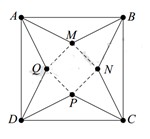
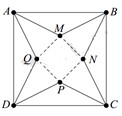
Giả sử M N = x ⇒ d A ; M Q = 5 2 − x 2 0 < x < 5 2
Chiều cao hình chóp là h = 5 2 − x 2 2 − x 2 2 = 50 − 10 x 2 4
Ta có V = 1 3 M N 2 . h = 1 3 x 2 50 − 10 x 2 4 = 1 6 50 x 4 − 10 x 5 2
Đặt
f x = 50 x 4 − 10 x 5 2 ⇒ f ' x = 2 − − x 3 − 50 x 3 2 = 0 ⇒ x = 2 2 d m
Lập bảng BTT suy ra V m a x = 2 2 d m