Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

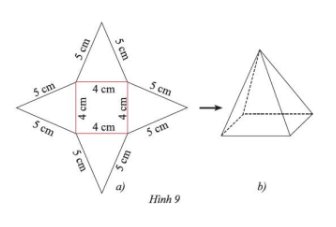
Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như Hình 9b.

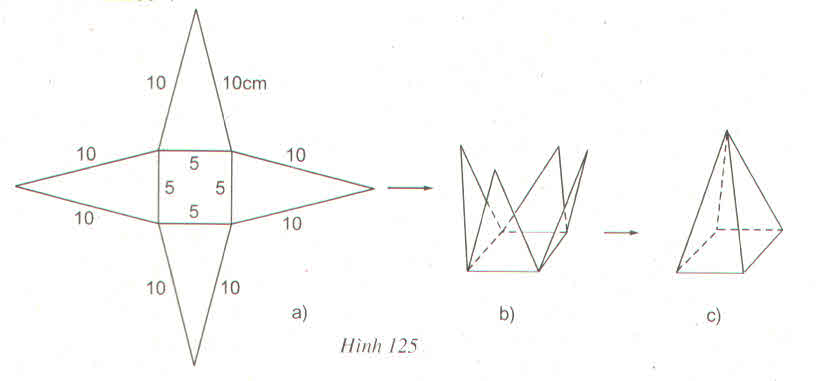
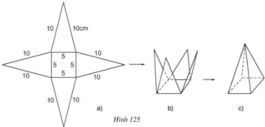
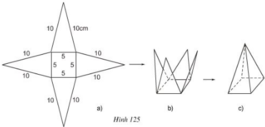
a) Trong hình 125a có 4 tam giác cân bằng nhau.
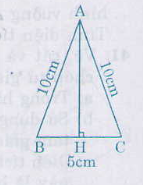
b) Chiều cao ứng với đáy của mỗi tam giác:
\(AH=\sqrt{AC^2-HC^2}\)
\(=\sqrt{AC^2-\left(\dfrac{1}{2}.5\right)^2}=\sqrt{100-\dfrac{25}{4}}=9,68\left(cm\right)\)
c) Diện tích xung quanh hình chóp:
Sxq = pd = \(\dfrac{1}{2}\).5.4.9,68 = 96,8 (cm2 )
Diện tích đáy:
Sđ = 52 = 25 (cm2 )
Diện tích toàn phần của hình chóp:
Stp = Sxq + Sđ = 121,8 (cm2 )

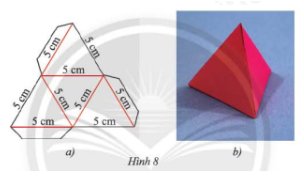
- Trên một tấm bìa, vẽ 4 hình tam giác đều với kích thước như Hình 8a.
- Cắt tấm bìa theo đường màu đen rồi gấp theo đường màu đỏ của Hình 8a.
- Sau khi gấp xong thu được hộp quà như Hình 8b

a) Đáy của hình lăng trụ đứng là một tam giác vuông cân
b) Các mặt bên nhận được không phải tất cả là hình vuông
\(\Bigg(\) hai hình vuông và một hình chữ nhật \(\Bigg)\)

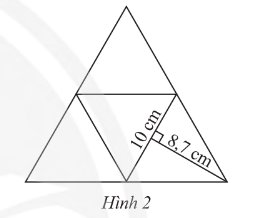
Diện tích một mặt của hình chóp là: \(10.8,7:2 = 43,5\) (\(c{m^2}\))
Diện tích xung quanh của hình chóp là: \(43,5.3 = 130,5\) (\(c{m^2}\))
Diện tích toàn phần của hình chóp là: \(43,5.4 = 174\) (\(c{m^2}\))

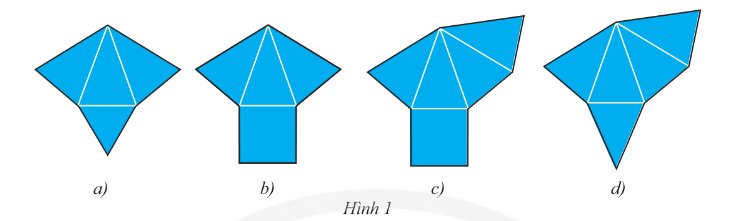
1a gấp được thành hình chóp tam giác đều
1c gấp được thành hình chóp tứ giác đều

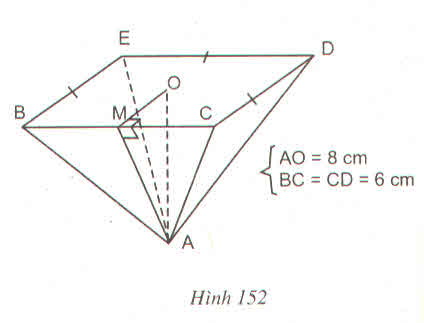
a) Trong hình 125a có 4 tam giác cân bằng nhau.
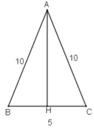
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.
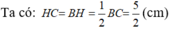
Chiều cao ứng với đáy của mỗi tam giác:
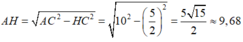
c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).
Diện tích xung quanh hình chóp:
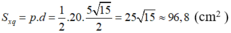
Diện tích đáy: Sd = 52 = 25 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sd + Sxq = 121,8 (cm2)

a) Trong hình 125a có 4 tam giác cân bằng nhau.
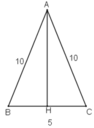
b) Gọi H là trung điểm BC. Tam giác ABC có AH là đường trung tuyến nên đồng thời là đường cao.
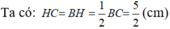
Chiều cao ứng với đáy của mỗi tam giác:
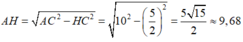
c) Chu vi đáy của hình chóp là 4.5 = 20 (cm).
Diện tích xung quanh hình chóp:
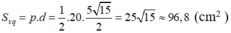
Diện tích đáy: Sd = 52 = 25 (cm2)
Diện tích toàn phần của hình chóp:
Stp = Sd + Sxq = 121,8 (cm2)
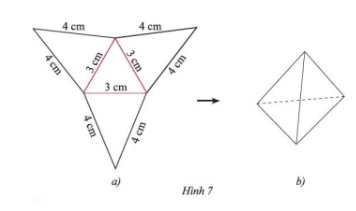


Sau khi thực hiện theo hướng dẫn, ta được sản phẩm như hình 7b.