Cho năm điểm G, H, I, K, L sao cho: ba điểm G, H, I thẳng hàng; ba điểm H, I, K thẳng hàng; ba điểm I, K, L không thẳng hàng.
Hỏi bốn điểm G, H, I, K có thẳng hàng hay không? Vì sao?
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ba điểm G, I, L không thẳng hàng vì hai điểm G, I thuộc đường thẳng HI mà điểm L không thuộc đường thẳng HI

a) Vì BC=2AB nên:\(\widehat{ABC}=2\widehat{ACB}\) mà \(\Delta ABC\) vuông nên \(\widehat{ABC} +\widehat{ACB}=90^o\)
\(\Rightarrow\)\(\widehat{ABC}=60^o,\widehat{ACB}=30^o\)
Suy ra:
\(\widehat{ABD}=20^o,\widehat{ACE}=10^o,\widehat{ECB}=20^o\).
C thuộc đường trung trực của của FH và FG nên CH=CG. Tam giác CGH cân tại C.
\(\widehat{GCH}=\widehat{GCF}+\widehat{FCH}=2\widehat{ACB}=60^o\)
Vậy tam giác GCH là tam giác đều, Do đó \(\widehat{CHG}=60^o(1)\)
\(\Delta CDH=\Delta CDF\)(c-g-c),suy ra \(\widehat{CHD}=\widehat{CFD}\)
tam giác vuông ABD vuông ở A có \(\widehat{ABD}=20^o\) nên \(\widehat{ADB}=70^o\) , suy ra \(\widehat{FDC}=110^o\) vì thế \(\widehat{DFC}=180^o-110^o-10^o=60^o\).vậy \(\widehat{CHD }=60^o(2)\)
từ (1) và (2) ta suy ra ba điểm M,D,C thẳng hàng
b) Gọi S là giao điểm các phân giác của tamgiacs BFC.ta dễ dàng chwungs minh được \(\widehat{EFB}=\widehat{BFS}=\widehat{SFC}=\widehat{DFC}=60^o\).
\(\Delta BFE=\Delta BFS(g-c-g)\) suy ra FE=FS(hai cạnh tương ứng)
\(\Delta CFS=\Delta CFD(g-c-g)\) suy ra FS=FD
từ hai chứng minh trên suy ra FE=FD.vậy tam giác EFD cân ở F

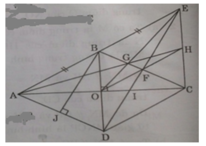
b) Xét Δ BCD có: O là trung điểm của BD
F là trung điểm của BC
⇒ OF là đường trung bình của ΔBDC ⇒ OF // DC mà DC // AB nên OF // AE
⇒ FH // BE
Mà O là trung điểm của AC nên H là trung điểm của EC hay AH là trung tuyến của ΔAEC. Mà AH cắt EO tại G nên G là trong tâm của ΔAEC ⇒ A, G, H thẳng hàng.
Bốn điểm G, H, I, K có thẳng hàng vì cả bốn điểm thuộc đường thẳng HI