Biết rằng khi m = m 0 thì hàm số f(x) = x+( m 2 − 1) x 2 + 2x + m − 1 là hàm số lẻ. Mệnh đề nào sau đây đúng?
A. m 0 ∈ ( 1 2 ; 3 )
B. m 0 ∈ [ - 1 2 ; 0 )
C. m 0 ∈ ( 0 ; 1 2 ]
D. m 0 ∈ [ 3 ; + ∞ )
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn đáp án D
Tập xác định:D = R .
Ta có ∀ x ∈ D ⇒ - x ∈ D .
Để f(x) là hàm số lẻ thì f - x = - f x .
![]()
![]()
![]()
![]()
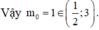

\(y'=0\Leftrightarrow4x^3-4x=0\Leftrightarrow4x\left(x^2-1\right)=0\\ \Leftrightarrow x=\pm1.và.x=0\)
\(HSNB:\left(-\infty;-1\right)\cup\left(0;1\right)\\ HSĐB:\left(-1;0\right)\cup\left(1;+\infty\right)\)

Chọn A
Phương pháp:
Nếu f ' ( x ) ≥ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) đồng biến trên khoảng (a;b).
Nếu f ' ( x ) ≤ 0 , ∀ x ∈ a ; b và chỉ bằng 0 tại hữu hạn điểm trên đó thì f(x) nghịch biến trên khoảng (a;b) Cách giải:
Quan sát đồ thị hàm số y=f’(x) , ta thấy f’(x) >0 =>Hàm số f (x) đồng biến trên
khoảng (-1;1).
=>Mệnh đề ở câu A là sai.
Đáp án A