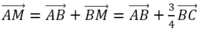Cho tam giác ABC . Gọi M là điểm trên cạnh AB sao cho MB = 3MA. Khi đó, biễu diễn A M → theo A B → và A C → là:
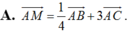
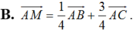
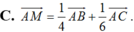
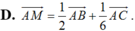
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Dùng kết quả: Nếu B, C, M thẳng hàng và A M → = x A B → + y A C → thì x + y = 1 để loại các phương án A, B, D.
Đáp án C

a, tu ve hinh :
tamgiac ABC can tai A => AB = AC va goc ABC = goc ACB (gn)
goc AIC = goc AIB = 90 do AI | BC (gt)
=> tamgiac AIC = tamgiac AIB (ch - gn)
=> IB = IC (dn)
b, dung PY-TA-GO
c, AE = AF (gt) => tamgiac AFE can tai E (dn)
=> goc AFE = (180 - goc BAC) : 2 (tc)
tamgiac ABC can tai A (gt) => goc ACB = (180 - goc BAC) : 2 (tc)
=> goc AFE = goc ACB ma 2 goc nay dong vi
=> EF // BC (dh)
vay_

Chắc bạn ghi nhầm, phải là \(\overrightarrow{CM}\) theo \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\) mới hợp lý, chứ M thuộc AB nên hiển nhiên rằng \(\overrightarrow{AM}=\frac{1}{4}\overrightarrow{AB}+0.\overrightarrow{AC}\)

a: Xét ΔMDB và ΔMEF có
MD=ME
góc DMB=góc EMF
MB=MF
=>ΔMDB=ΔMEF
b: ΔMDB=ΔMEF
=>DB=EF
=>EC=EF
=>ΔECF cân tại E

Ta có M B → = 1 3 M C → ⇔ 3 M B → = M C → ⇔ 3 B M → = C M →
A M → = A B → + B M → ⇒ 3 A M → = 3 A B → + 3 B M → ( 1 ) A M → = A C → + C M → ( 2 )
Lấy (1) trừ (2) ta được :
2 A M → = 3 A B → + 3 B M → − A C → + C M → = 3 A B → − A C → + ( 3 B M → − C M → ) = 3 A B → − A C → + 0 → = 3 A B → − A C → ⇒ A M → = 3 2 A B → − 1 2 A C → = 3 2 u → − 1 2 v →
Đáp án A

a) \(\overrightarrow{MN}=\overrightarrow{MA}+\overrightarrow{AN}=\dfrac{-1}{2}\overrightarrow{AB}+\dfrac{1}{3}\overrightarrow{AC}\)
b) CG.CAN??

a: Xét ΔMDB và ΔMEF có
MD=ME
góc DMB=góc EMF
MB=MF
=>ΔMDB=ΔMEF
b: ΔMDB=ΔMEF
=>DB=EF
=>EC=EF
=>ΔECF cân tại E

a: Xét ΔMDB và ΔMEF có
MD=ME
góc DMB=góc EMF
MB=MF
=>ΔMDB=ΔMEF
b: ΔMDB=ΔMEF
=>DB=EF
=>EC=EF
=>ΔECF cân tại E
Chọn B.
Ta có