Cho hai đường thẳng song song a; b. Trên đường thẳng a lấy 10 điểm phân biệt, trên b lấy 15 điểm phân biệt. Hỏi có bao nhiêu tam giác mà ba đỉnh của nó được chọn từ 25 vừa nói trên.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hai đường thẳng song song là hai đường thẳng không có điểm chung
a. Đúng
b. sai (vì hai đường thẳng không cắt nhau có thể trùng nhau)
c. Đúng
d. Đúng

a) Đúng
b) Sai. Vì hai đường thẳng không cắt nhau có thể song song hoặc trùng nhau.
c) Đúng
d) Đúng
e) Đúng
f) Đúng

Không vì trái với định lí ( a // b thì a và b không cắt nhau)

Sử dụng êke
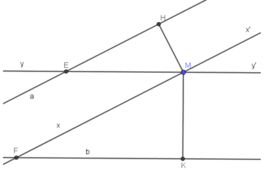
* Để vẽ đường thẳng xx’ đi qua M và song song với a, ta chỉ cần vẽ đường thẳng vuông góc với MH.
Thật vậy vì xx’ ⏊ MH, MH ⏊ a ⇒ xx’ // a.
Cách vẽ:
Đặt ê ke sao cho đỉnh góc vuông trùng với điểm M, một cạnh góc vuông trùng với MH.
Vẽ đoạn thẳng trùng với cạnh góc vuông còn lại của eke.
Kéo dài đoạn thẳng ta được đường thẳng xx’ cần vẽ.
* Tương tự với đường thẳng yy’

Số tam giác lập được thuộc vào một trong hai loại sau
Loại 1: Gồm hai đỉnh thuộc vào a và một đỉnh thuộc vào b
Số cách chọn bộ hai điểm trong 10 thuộc a: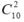
Số cách chọn một điểm trong 15 điểm thuộc b: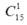
Loại này có: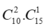 tam giác.
tam giác.
Loại 2: Gồm một đỉnh thuộc vào a và hai đỉnh thuộc vào b
Số cách chọn một điểm trong 10 thuộc a: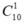
Số cách chọn bộ hai điểm trong 15 điểm thuộc b: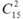
Loại này có: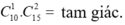
Vậy có tất cả: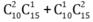 tam giác thỏa yêu cầu bài toán
tam giác thỏa yêu cầu bài toán
Chọn C.