Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án C
Ta có: y ' = 4 x 3 − 4 x = 4 x x 2 − 1 > 0 ⇔ − 1 < x < 1 x > 1 ⇒ hàm số đồng biến trên các khoảng − 1 ; 0 và 1 ; + ∞ .
Đáp án B
y ' = - 4 x 3 + 4 x
y ' = 0 ⇔ - 4 x 3 + 4 x = 0 ⇔ x ∈ - 1 , 0 , 1
Suy ra hàm số đồng biến trong - ∞ , - 1 v à 0 , 1
Đáp án D
Ta có: y ' = 4 x 3 − 4 x = 4 x x 2 − 1 > 0 ⇔ x ∈ − 1 ; 0 ∪ 1 ; + ∞ ⇒ Hàm số đồng biến trên các khoảng − 1 ; 0 và 1 ; + ∞
Đáp án C.
Hàm số y = -x4 + 2x2 có y’ = -4x3 + 4x, y’ ≥ 0
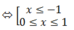
Vậy hàm số đã cho đồng biến trên (-∞; -1)
Đáp án D.
y = x4 – 2x2 + 3 => y’ = 4x3 – 4x.
y’ = 0 <=> 4x3 – 4x = 0 <=>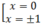
Vậy hàm số đồng biến trên khoảng (-1 ;0) và (1; +∞).