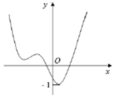
Cho hàm số y= f( x) có đồ thị như hình vẽ bên Tìm số điểm cực trị của hàm số y= 2f( x) – 3f( x) A. 6 B. 5 C. 4 D....
Đọc tiếp
Cho hàm số y= f( x) có đồ thị như hình vẽ bên
Tìm số điểm cực trị của hàm số y= 2f( x) – 3f( x)
A. 6
B. 5
C. 4
D. 3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
19 tháng 4 2017
Đáp án B
f'(x) đổi dấu 1 lần, suy ra đồ thị hàm số f(x) có 1 điểm cực trị.
CM
5 tháng 3 2018
Đáp án C
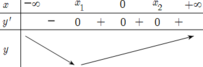
Khi đó hàm số y=f(x) đạt cực tiểu tại x = x 1 hay hàm số y=f(x) có 1 điểm cực trị.
CM
13 tháng 1 2018
Đáp án D
Phương pháp giải:
Tính đạo hàm của hàm số và tìm nghiệm của phương trình y'=0 dựa vào bài toán tương giao và đồ thị hàm số y=f(x) =>Số điểm cực trị của hàm số cần tìm.
Lời giải:
xét hàm số
Dựa vào đồ thị hàm số y = f(x), ta thấy:
Phương trình (1) có 3 nghiệm phân biệt (vì hàm số y = f(x) có 3 điểm cực trị).
Phương trình (2) vô nghiệm vì đường thẳng y = log 2 3 ln 3 ln 2 < − 1 không cắt ĐTHS.
Vậy phương trình g'(x) = 0 có 3 nghiệm phân biệt hay hàm số đã cho có 3 điểm cực trị.
CM
1 tháng 6 2019
Đặt h( x) = 2f( x) – ( x-1) 2
Suy ra đạo hàm: h’( x) = 2f’(x) -2( x-1).
Ta vẽ thêm đường thẳng y= x-1.
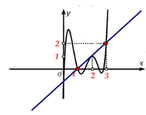
Ta có h’ (x) =0 khi f’(x) =x-1
Suy ra x=0; x=1; x=2; x=3
Theo đồ thị h’(x) > .0 khi f’(x) > x-1
Ta có :
Đồ thị hàm số g( x) có nhiều điểm cực trị nhất khi h( x) có nhiều giao điểm với trục hoành nhất.
Vậy đồ thị hàm số h( x) cắt trục hoành tại nhiều nhất 4 điểm, suy ra đồ thị hàm số g(x) có tối đa 7 điểm cực trị.
Chọn B.
CM
4 tháng 9 2018
Đáp án B.
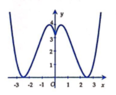
Hàm số y = f x + m là một hàm số chẵn nên đồ thị đối xứng qua trục Oy. Mặt khác y = f x + m = f x + m ∀ x ≥ 0 . Ta có phép biến đổi từ đồ thị hàm số y = f x thành đồ thị hàm số y = f x + m :
* Nếu m > 0:
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang trái m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
* Nếu m=0 :
- Bước 1: Tịnh tiến đồ thị hàm số y = f x sang phải m đơn vị.
- Bước 2: Xóa phần nằm bên trái Oy của đồ thị thu được ở Bước 1.
- Bước 3: Lấy đối xứng đồ thị thu được ở Bước 2 qua Oy.
Quan sát ta thấy đồ thị hàm số y = f x có 2 điểm cực trị.
Để đồ thị hàm số y = x + m có 5 điểm cực trị thì nhánh bên phải Oy của đồ thị hàm số y = x + m phải có 2 điểm cực trị => Điểm cực trị của đồ thị hàm số y = f x phải được tịnh tiến sang phải O y ⇒ m < − 1 .
Xét hàm số
Dựa vào đồ thị hàm số y= f( x) , ta thấy:
Phương trình (1) có 3 nghiệm phân biệt (vì hàm số y= f (x) có 3 điểm cực trị).
Phương trình (2) vô nghiệm vì đường thẳng y = log 2 3 ln 3 ln 2 < - 1 không cắt ĐTHS.
Vậy phương trình g’ (x) =0 có 3 nghiệm phân biệt hay hàm số đã cho có 3 điểm cực trị.
Chọn D.