Cho hàm số y= f( x) đạo hàm f’ (x) = -x2- 1. Với các số thực dương a, b thỏa mãn a< b. Giá trị nhỏ nhất của hàm số f( x) trên đoạn [ a; b] bằng
A. f(a)
B. f a b
C. f( b)
D. f a + b 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Phương pháp giải:
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Lời giải:
Ta có ![]() suy ra f(x) là hàm số nghịch biến trên [a;b]
suy ra f(x) là hàm số nghịch biến trên [a;b]
Mà ![]() . Vậy
. Vậy ![]()

Chọn A
Hàm số y = f(x) thỏa mãn f'(x) < 0 ∀ x ∈ ( a ; b ) nên hàm số nghịch biến trên (a;b).
Do đó ![]()

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.

Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.

Ta có
![]()
![]()
![]()
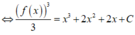
![]()
Ta có: f ( 0 ) = 1 ⇒ 1 = 3 C
![]()
![]()
Xét hàm ![]() trên [-2;1]
trên [-2;1]
Ta có
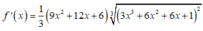
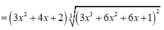
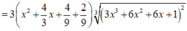
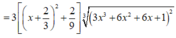
Nhận thấy f ' ( x ) > 0 ∀ x ∈ ℝ ⇒ Hàm số đồng biến trên (-2;1)
Suy ra m a x - 2 ; 1 f ( x ) = f ( 1 ) = 16 3
Chọn đáp án C.
Hàm số đơn điệu trên đoạn nên giá trị nhỏ nhất – lớn nhất sẽ đạt tại đầu mút của đoạn
Ta có f’ (x) = -x2-1< 0 với a< x< b ; suy ra hàm số y= f( x) là hàm số nghịch biến trên [ a; b].
Mà a< b nên f(a) > f( b)
Vậy m i n [ a ; b ] f ( x ) = f ( b )
Chọn C.