Tính tổng các giá trị nguyên của m để hàm số y= x8+ (m-2) x5- ( m2- 4) x4+ 1 đạt cực tiểu tại x= 0
A. 3.
B. 5.
C. 4.
D. 2.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ND
Nguyễn Đức Trí
VIP
9 tháng 8 2023
\(y=x^8+\left(m-2\right)x^5-4\left(m^2-4\right)+1\)
Tập xác định \(D=ℝ\)
\(y'=8x^7+5\left(m-2\right)x^4\)
\(y''=56x^6+20\left(m-2\right)x^3\)
Để hàm số đạt cực tiểu tại \(x=0\)
\(\left\{{}\begin{matrix}y'\left(0\right)=0\\y''\left(0\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}0m=0\\0m>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}\forall m\inℝ\\m>0\end{matrix}\right.\) \(\Leftrightarrow m>0\)
Vậy \(m>0\) hàm số trên đạt cực tiểu tại \(x=0\)
TD
9 tháng 8 2023
Với đề thi THPT quốc gia môn Toán, đây là một trong những câu khó. Không nhiều các bạn học sinh giải được đề toán trên. Đây là một hàm số bậc 8, hoàn toàn khác với những hàm số thông dụng được học trên lớp, để giải được bài này, các bạn cần phải sử dụng kiến thức từ định nghĩa và tính chất của cực trị hàm số bất kì. Ta có:
y" = 8x7 + 5(m - 2)x4 - 4(m2 - 4)x3 + 1
Hàm đạt cực tiểu tại x = 0 thì y"(x) = 0 và y"(x) đổi dấu từ âm sang dương khi x chạy qua điểm 0. Từ đó ta tương đương với số hạng chứa x có lũy thừa thấp nhất có hệ số khác 0 trong biểu thức y’ là lũy thừa bậc lẻ, hệ số dương.
Có nghĩa là :
–4(m2 - 4) > 0 và m - 2 = m² – 4 = 0
⇔ –2 Bài 2 - Mã đề 124 đề thi môn Toán THPT Quốc gia 2017
Dưới đây là hàm số y = f(x) được thể hiện trong bình với bảng biến thiên:
Tìm giá trị cực tiểu, cực đại của hàm số đã cho.
Bài giải:
Theo như bảng biến thiên các em học sinh nhận thấy được cực tiểu là 0 và giá trị cực đại của hàm số là 3.
Nhiều câu hỏi cho sẵn bảng biến thiên hay hình vẽ đồ thị hàm số sẽ xuất hiện trong đề thi. Chúng ta có thể vận dụng chính những dữ liệu này để có cho mình được đáp án đúng một cách nhanh chóng.
Đây nhé bro:))!
H
1
30 tháng 4 2022
Tham khảo
+ Ta có:
Ta xét các trường hợp sau
+ Nếu m2- 4= 0 hay m= ± 2
Khi m = 2 thì y’ = 8x7 nên x=0 là điểm cực tiểu.
Khi m = -2 thì y’ = x4( 8x4- 20 ) khi đó x= 0 không là điểm cực tiểu.
+ Nếu m ≠ ± 2 .Khi đó ta có
Số cực trị của hàm y = x8+ (m-2) x5- ( m2- 4) x4+ 1 bằng số cực trị của hàm g’( x)
+) Nếu x = 0 là điểm cực tiểu thì g’’ (0) > 0.
Khi đó: -4( m2 - 4) > 0 hay -2 < m < 2
Mà m nguyên nên m= -1; 0; 1
Kết hợp cả 2 trường hợp có 4 giá trị nguyên của m và tổng của chúng là:
2 + ( -1) + 0 + 1 = 2
CM
24 tháng 7 2017
Đáp án C.
Ta có y ' = 4 x 3 − 4 m + 1 x = 4 x x 2 − m − 1 .
Hàm trùng phương với hệ số a > 0 có 2 dạng:
+) Có 2 cực tiểu và 1 cực đại tại x = 0 ⇒ y ' = 0 có 3 nghiệm phân biệt.
+) có 1 cực tiểu tại x = 0 ⇒ y ' = 0 có 1 nghiệm x = 0.
Hàm số đã cho đạt cực tiểu tại x = 0 ⇔ m + 1 ≤ 0 ⇔ m ≤ − 1.
CH
2
10 tháng 8 2021
Tìm tất cả các giá trị nguyên của m để hàm số y=x^8+(m-2)x^5-(m^2-4)x^4+1 đạt cực tiểu tại x=0.
m= 2
nha bạn
bạn muốn tl rõ hơn thì bạn tìm trên google
CM
26 tháng 12 2017
Đáp án B
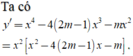
Dễ thấy x=0 là một nghiệm của đạo hàm y'. Do đó hàm số đạt cực tiểu tại x=0 khi và chỉ khi y'đổi dấu từ âm sang dương khi đi qua nghiệm x=0.Ta thấy dấu của y' là dấu của hàm số g ( x ) = x 2 - 4 2 m - 1 x - m . Hàm số g(x) đổi dấu khi đi qua giá trị x=0 khi x=0 là nghiệm của g(x). Khi đó g(0) = 0 ⇔ m=0
Thử lại, với m=0 thì g ( x ) = x 2 + 4 x đổi dấu từ âm sang dương khi đi qua giá trị x=0
Vậy có 1 giá trị m thỏa mãn yêu cầu bài toán
CM
4 tháng 12 2017
Đáp án C.
y' = x2 – 2x + m2 – 4
Để hàm số đạt cực tiểu tại x = 3 ó y’(3) = 0 ó m2 – 1 = 0 ó m = ±1
+ Ta có:
Ta xét các trường hợp sau
+ Nếu m2- 4= 0 hay m= ± 2
Khi m= 2 thì y’ = 8x7 nên x=0 là điểm cực tiểu.
Khi m=y’ = x4( 8x4- 20 ) khi đó x= 0 không là điểm cực tiểu.
+ Nếu m ≠ ± 2 .Khi đó ta có
Số cực trị của hàm y= x8+ (m-2) x5- ( m2- 4) x4+ 1 bằng số cực trị của hàm g’( x)
+Nếu x= 0 là điểm cực tiểu thì g’’ (0) >0.
Khi đó -4( m2- 4) > 0 hay -2< m< 2
Mà m nguyên nên m= -1; 0; 1
Kết hợp cả 3 trường hợp có 4 giá trị nguyên của m và tổng của chúng là:
2+ ( -1) +0+ 1=2
Chọn D.