Kí hiệu H là hình phẳng giới hạn bởi các đường y = e x , y = 0 , x = 0 và x = 1 . Đường thẳng x = k 0 < k < 1 chia H thành hai phần có diện tích tương ứng S 1 , S 2 như hình vẽ bên, biết S 1 > S 2 . Mệnh đề nào sau đây là đúng?
A. e k > e - 1 2
B. e k > e + 1 2
C. e k > e + 2 2
D. e k > e + 3 2

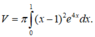
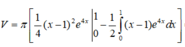
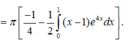
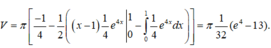
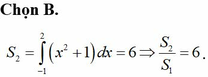
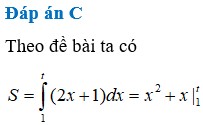


Ta có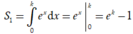 và
và 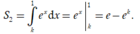
Theo giả thiết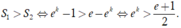
Chọn B.