Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
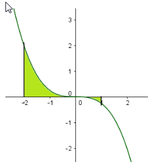
Do f 0 < 0 < f − 1 nên phương trình f x = 0 có ít nhất 1 nghiệm x ∈ − 1 ; 0
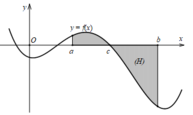
Đáp án đúng là S = ∫ − 1 1 f x d x

Chọn C
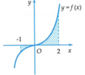
Diện tích hình phẳng giới hạn bởi các đường y = l x , y = 0 , x = 0 , x = 2 được tính theo công thức S = ∫ 0 2 l x d x = ∫ 0 2 l x d x
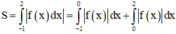
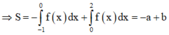
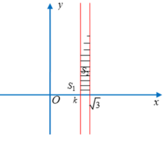
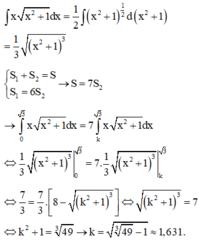
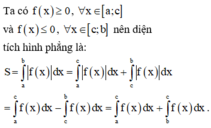
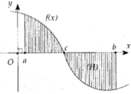

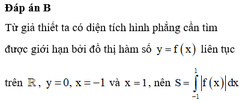
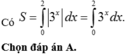
Ta có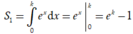 và
và 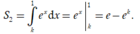
Theo giả thiết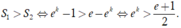
Chọn B.