Tính tổng các giá trị của tham số m sao cho đường thẳng y = x cắt đồ thị hàm số y = x - 5 x + m tại hai điểm A và B sao cho AB = 4 2
A. 2
B. 5
C. 7
D. 8
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Phương trình hoành độ giao điểm x = x − 5 x + m ⇔ x + m ≠ 0 x 2 + m − 1 x + 5 = 0 1
Hai đồ thị có 2 giao điểm ⇔ 1 có 2 nghiệm phân biệt x ≠ − m
Suy ra Δ = m − 1 2 − 20 > 0 − m 2 − m m − 1 + 5 ≠ 0 ⇔ m > 2 5 + 1 m < 1 − 2 5 m ≠ − 5 *
Khi đó
x A + x B = 1 − m x A x B = 5 ⇒ A B = 2 x A − x B 2 = 2 x A + x B 2 − 8 x A x B = 2 1 − m 2 − 40 = 4 2
⇒ 2 1 − m 2 − 40 = 32 ⇒ m − 1 2 = 36 ⇔ m = 7 m = − 5
Kết hợp điều kiện * ⇒ m = 7

Phương trình hoành độ giao điểm:
\(x^2+3x=x+m^2\Leftrightarrow x^2+2x-m^2=0\)
Pt đã cho luôn có 2 nghiệm pb
\(\left\{{}\begin{matrix}x_1+x_2=-2\\x_1x_2=-m^2\end{matrix}\right.\)
Do I là trung điểm đoạn AB \(\Leftrightarrow\left\{{}\begin{matrix}x_I=\dfrac{x_A+x_B}{2}=-1\\y_I=\dfrac{y_A+y_B}{2}=\dfrac{x_A+m^2+x_B+m^2}{2}=m^2-1\end{matrix}\right.\)
Mà I thuộc d'
\(\Leftrightarrow y_I=2x_I+3\Leftrightarrow m^2-1=2.\left(-1\right)+3\)
\(\Leftrightarrow m^2=2\Rightarrow m=\pm\sqrt{2}\)
\(\Rightarrow\sum m^2=4\)

Đáp án C
Xét pt tương giao:
2 x - 1 x - 1 = x + m ⇔ 2 x - 1 - x + m x - 1 = 0 ⇔ x 2 - 3 - m x + m - 1 = 0
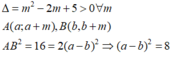
a + b 2 - 4 a b = 8 ⇔ 3 - m 2 - 4 1 - m = 8 ⇔ [ m = - 1 m = 3

Đáp án DPhương trình hoành độ gaio điểm của đồ thị (C) và đường thẳng 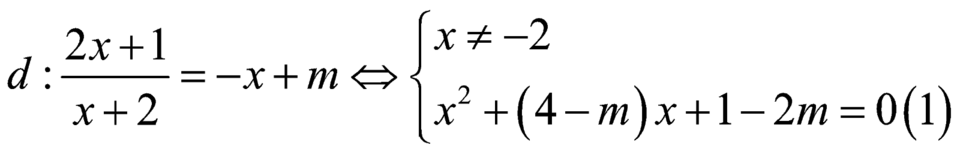
Gọi ![]() . Ta tính được
. Ta tính được ![]() khi m = 0
khi m = 0
Phương trình hoành độ giao điểm
x x + m = x - 5 x ≠ - m ⇔ x 2 + m - 1 x + 5 = 0 = f x x ≠ - m
Đường thẳng cắt đồ thị tại 2 điểm A,B khi và chỉ khi
∆ 1 > 0 f - m ≠ 0 ⇔ m 2 - 2 m - 19 > 0 m ≠ - 5
Gọi A x 1 ; x 1 , B x 2 ; x 2 với x 1 ; x 2 là 2 nghiệm của phương trình f(x) = 0
A B = 4 2 ⇔ x 2 - x 1 = 4 ⇔ x 1 + x 2 2 - 4 x 1 x = 16 ⇔ m 2 - 2 m - 35 = 0 ⇔ m = 7 m = - 5
So với điều kiện ta nhận m = 7
Đáp án C