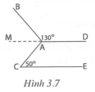
Hình 3.7 có B A D ^ = 130 ° , C ^ = 50 ° . Vẽ tia AM là tia đối của tia AD. Biết tia AM là tia phân giác của góc BAC. Chứng tỏ rằng AD // CE.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Ta có: \(\widehat{BAC}+\widehat{EAC}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{EAC}+60^0=180^0\)
hay \(\widehat{EAC}=120^0\)
Vậy: \(\widehat{EAC}=120^0\)
b)
Ta có: AD là tia phân giác của \(\widehat{CAE}\)(gt)
nên \(\widehat{EAD}=\widehat{CAD}=\dfrac{\widehat{EAC}}{2}=\dfrac{120^0}{2}=60^0\)
Ta có: \(\widehat{EAD}+\widehat{BAD}=180^0\)(hai góc kề bù)
\(\Leftrightarrow\widehat{BAD}+60^0=180^0\)
hay \(\widehat{BAD}=120^0\)
Trên cùng một nửa mặt phẳng bờ chứa tia AB, ta có: \(\widehat{BAC}< \widehat{BAD}\left(60^0< 120^0\right)\)
nên tia AC nằm giữa hai tia AB và AD
Ta có: tia AC nằm giữa hai tia AB và AD(cmt)
mà \(\widehat{BAC}=\widehat{DAC}\left(=60^0\right)\)
nên AC là tia phân giác của \(\widehat{BAC}\)(Đpcm)

a: ΔBAC vuông tại B
=>\(\widehat{BAC}+\widehat{BCA}=90^0\)
=>\(2\left(\widehat{IAC}+\widehat{ICA}\right)=90^0\)
=>\(\widehat{IAC}+\widehat{ICA}=45^0\)
Xét ΔIAC có \(\widehat{IAC}+\widehat{ICA}+\widehat{CIA}=180^0\)
=>\(\widehat{CIA}=180^0-45^0=135^0\)
b: CI và CK là hai tia phân giác của hai góc kề bù
=>\(\widehat{ICK}=90^0\)
\(\widehat{CIK}+\widehat{CIA}=180^0\)
=>\(\widehat{CIK}=45^0\)
Xét ΔCKI vuông tại C có \(\widehat{CIK}=45^0\)
nên ΔCKI vuông cân tại C
=>\(\widehat{CKI}=\widehat{CKA}=45^0\)

Vì AD là phân giác BAC => DAC = DAB = BAC : 2 hay 2DAC = 2DAB = BAC
Vì CE là phân giác BCA => BCE = ECA = BCA : 2 hay 2BCE = 2ECA = BCA
Xét △ABC vuông tại B có: BAC + BCA = 90o (2 góc nhọn trong △ vuông)
=> 2DAC + 2ECA = 90o => DAC + ECA = 45o
Xét △ICA có: ICA + IAC + CIA = 180o (tổng 3 góc trong tam giác)
=> 45o + CIA = 180o => CIA = 135o
b, Xét △ABC có BCx là góc ngoài của △ tại đỉnh C, ta có: BCx = CBA + BAC => BCx = 90o + BAC
Vì CK là phân giác BCx \(\Rightarrow\frac{\widehat{BCx}}{2}=\frac{90^o+\widehat{BAC}}{2}\)\(\Rightarrow\widehat{BCK}=45^o+\widehat{DAC}\)
Xét △KCA có: CKA + KCA + CAK = 180o (tổng 3 góc trong △)
=> CKA + KCD + DCI + ICA + CAK = 180o
=> CKA + 45o + DAC + DCI + ICA + CAK = 180o
=> CKA + (DAC + ICA) + (DCI + CAK) = 135o
=> CKA + 45o + 45o = 135o
=> CKA = 45o

a, Có ^cAe + ^cAd = 180o (kề bù) => ^cAe = 120o
b,Vì Ad là p/g ^cAe => ^A1 = ^A2 = \(\frac{\widehat{cAe}}{2}=\frac{120^o}{2}=60^o\)
Ta có : \(\widehat{A_1}+\widehat{bAd}=180^o\)(Kề bù)
\(\Rightarrow\widehat{bAd}=120^o\)
\(\Rightarrow\widehat{bAd}>\widehat{bAc}\left(120^o>60^o\right)\)
Mà ^bAd = 2.^bAc
=> Ac là p/g ^bAd
c,Có ^cAe + ^A4 = 180o (kề bù)
=> ^A4 = 60o
Có ^bAg + ^A4 = 180 (kề bù)
=>^bAg = 120o
Vì AH là p/g ^bAg => ^A5 = ^bAg : 2 = 60o
Ta có \(\widehat{A_1}+\widehat{A_4}+\widehat{A_5}=60^o+60^o+60^o=180^o\)
=> ^dAh = 180o
=> 2 tia Ad và Ah đối nhau


a) B A C ^ + B A D ^ = 180 0 mà B A C ^ =80 0 nên B A D ^ = 100 0
Tia AM là tia phân giác của góc BAD nên Â1=1000: 2 = 500.
Ta có : A 1 ^ = D ^ = 50 0 suy ra DE//AM( Vì có cặp góc so le trong bằng nhau).
b) Ta có : A 1 ^ = C ^ = 50 0
suy ra BC//AM (Vì có cặp góc đồng vị bằng nhau).
Tìm cách giải
Đề bài có cho hai tia đối nhau nên ta vận dụng tính chất của hai góc kề bù. Ngoài ra đề bài còn có tia phân giác nên trong hình vẽ có hai góc bằng nhau.
Trình bày lời giải
Hai góc MAB và BAD kề bù nên M A B ^ = 180 ° − 130 ° = 50 ° .
Tia AM là tia phân giác của góc BAC nên M A C ^ = M A B ^ = 50 ° .
Do đó M A C ^ = C ^ = 50 ° ⇒ A D / / C E vì có cặp góc so le trong bằng nhau