Hai đường tròn phân biệt có cùng bán kính có bao nhiêu tâm đối xứng:
A. 0
B. 1
C. 2
D. vô số
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Giả sử vẽ được như hình bs.18
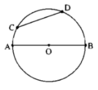
Với hai điểm (phân biệt) trên một đường tròn ta có được hai cung có mút là hai điểm đó. Với n điểm (phân biệt) cho trước trên một đường tròn, thì cứ lấy 2 trong số n điểm đó ta được 2 cung, vì vậy có tất cả n(n – 1) cung trên đường tròn đó.

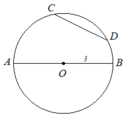
Với hai điểm (phân biệt) trên một đường tròn ta có được 2 cung có mút là hai điểm đó. Với n điểm (phân biệt) cho trước trên một đường tròn, thì cứ lấy 2 trong số n điểm đó ta được 2 cung, vì vậy có tất cả n(n-1) cung trên đường tròn đó.

a: Tên các cung là CA;AD;CB;DB
b: Vì AB là đường kính
và CD là dây
nên AB>CD
c: Ta sẽ được n(n-1) cung

Giải:
Áp dụng công thức sau \(\dfrac{n.\left(n-1\right)}{2}\) , ta làm như sau:
Số cung có các đầu mút là 2 trong số các điểm đó là:
\(\dfrac{4.\left(4-1\right)}{2}=6\) (cung)
Chúc bạn học tốt!
Đáp án B