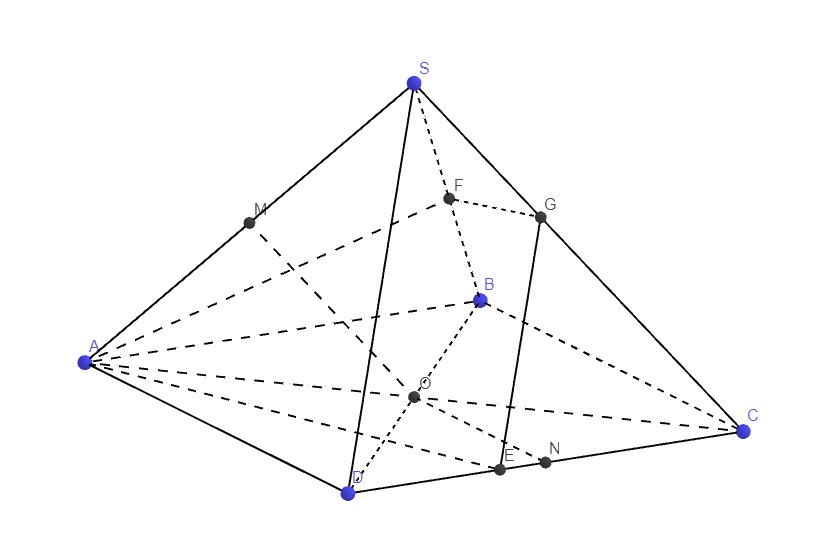
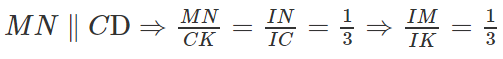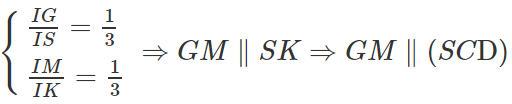Cho hình chóp S.ABCD với đáy ABCD là hình bình hành. Gọi lần lượt là trọng tâm của các tam giác SAD và SBC. Gọi M là giao điểm của SG và AD; N là giao điểm của SG’ và BC và O là giao điểm của BD và AN. Tìm giao tuyến của mặt phẳng (ADG’) và (SBD)
A. DI trong đó I là giao điểm của SO và AG’
B. DJ trong đó J là giao điểm của AG’ và SD
C. DH trong đó H là giao điểm của AD và BD
D. Tất cả sai

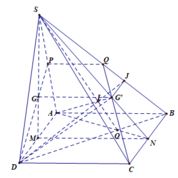

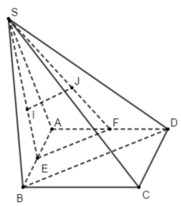
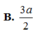
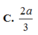
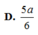


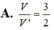
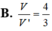
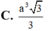
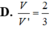

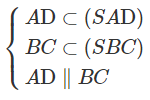
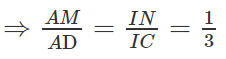
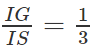
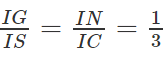 ⇒ GN // SC
⇒ GN // SC