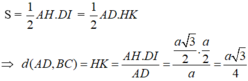Cho tứ diện đều ABCD cạnh a. Tính cosin góc giữa hai đường thẳng AB và CI với I là trung điểm của AD
A. 3 2
B. 3 6
C. 3 4
D. 1 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

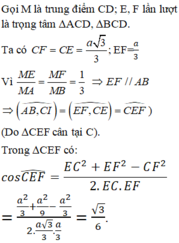


Đáp án A
Giả sử tứ diện đều cạnh a
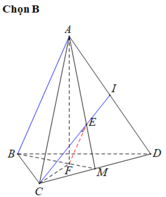
Gọi H là tâm đường tròn ngoại tiếp Δ B C D ⇒ A H ⊥ B C D
Gọi E là trung điểm
A C ⇒ M E // A B ⇒ A B , D M = M E , M D
Ta có M E = a 2 , E D = M D = a 3 2
cos
A
B
,
D
M
=
cos
M
E
,
M
D
=
cos
E
M
D
⏜
cos
E
M
D
⏜
=
M
E
2
+
M
D
2
−
E
D
2
2
M
E
.
M
D
=
3
6

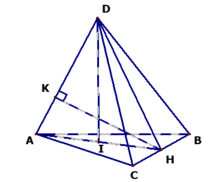
Tính khoảng cách giữa AD và BC.
● Trong ΔADH vẽ đường cao HK tức là HK ⊥ AD (1)
- Mặt khác BC ⊥ (ADH) nên BC ⊥ HK (2)
- Từ (1) và (2) ta suy ra d(AD, BC) = HK.
● Xét ΔDIA vuông tại I ta có:
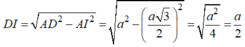
● Xét ΔDAH ta có: