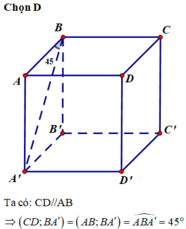
Cho hình lập phương ABCD.A’B’C’D’. Góc giữa hai đường thẳng BA’ và CD bằng
A. 90⁰.
B. 30⁰.
C. 60⁰.
D. 45⁰.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


\(\overrightarrow{DM}.\overrightarrow{A'N}=\left(\overrightarrow{DA}+\overrightarrow{AM}\right)\left(\overrightarrow{A'B'}+\overrightarrow{B'N}\right)\)
\(=\overrightarrow{DA}.\overrightarrow{A'B'}+\overrightarrow{AM}.\overrightarrow{A'B'}+\overrightarrow{DA}.\overrightarrow{B'N}+\overrightarrow{AM}.\overrightarrow{B'N}\)
( chứng minh được \(DA\perp A'B',AM\perp B'N\) )
\(=0+\dfrac{1}{2}\overrightarrow{AB}.\overrightarrow{AB}+\overrightarrow{C'B'}.\left(-\dfrac{1}{2}\overrightarrow{C'B'}\right)+0\)
\(=\dfrac{1}{2}AB^2-\dfrac{1}{2}C'B'^2=0\)
Suy ra \(DM\perp A'N\)
Ý A

Đáp án D
Gọi E là trung điểm A’B’. Khi đó ANC’E là hình bình hành. Suy ra C’N song song với AE. Như vậy góc giữa hai đường thẳng BM và C’N bằng góc giữa hai đường thẳng BM và AE. Ta có Δ M A B = Δ E A ’ A c − g − c suy ra A ' A E ^ = A B M ^ (hai góc tương ứng).
Do đó: A ' A E ^ + B M A ^ = A B M ^ + B M A ^ = 90 0 . Suy ra hai đường thẳng BM và AE vuông góc với nhau nên góc gữa chúng bằng 90 0 . Vậy góc giữa hai đường thẳng BM và C’N bằng 90 0 .
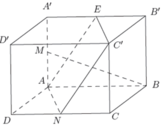

Đáp án D.
Phương pháp giải: Dựng hình để xác định góc giữa hai đường thẳng chéo nhau: Góc giữa hai đường thẳng a và b là góc giữa a’ và b với a // a’.
Lời giải: Vì ABCD là hình vuông ⇒ A C ⊥ B D mà A C / / A ' C ' ⇒ A ' C ' ⊥ B D

Đáp án D
Phương pháp giải: Dựng hình để xác định góc giữa hai đường thẳng chéo nhau : Góc giữa hai đường thẳng a và b là góc giữa a’ và b với a // a’.
Lời giải: Vì ABCD là hình vuông ⇒ A C ⊥ B D mà A C / / A ' C ' ⇒ A ' C ' ⊥ B D .

Vì CD // C’D’ nên góc giữa AC và C’D’ bằng góc giữa AC và CD – bằng góc ACD
Vì ABCD là hình vuông nên tam giác ACD vuông cân tại D
⇒ A C D ^ = 45 0
Đáp án B