4x2-12x+9
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
DT
0
N
2 tháng 10 2021
(2x + y)2 - (2x - 3)2 = (2x + y - 2x + 3)(2x + y + 2x - 3) = (y + 3)(4x + y - 3)
2 tháng 10 2021
\(\left(2x+y\right)^2-4x^2+12x-9\)
\(=\left(2x+y\right)^2-\left(2x-3\right)^2\)
\(=\left(2x+y-2x+3\right)\left(2x+y+2x-3\right)\)
\(=\left(y+3\right)\left(4x+y-3\right)\)
VH
5
HH
1
KN
26 tháng 7 2019
Đặt \(C=\sqrt{4x^2-4x+1}+\sqrt{4x^2-12x+9}\)
\(=\sqrt{\left(2x-1\right)^2}+\sqrt{\left(2x-3\right)^2}\)
\(=\left|2x-1\right|+\left|2x-3\right|\)
\(=\left|2x-1\right|+\left|3-2x\right|\)
\(\ge\left|\left(2x-1\right)+\left(3-2x\right)\right|=\left|2\right|=2\)
Vậy \(C_{min}=2\)
23 tháng 9 2021
a) Sửa đề: \(x^2+3x+1\rightarrow x^2+2x+1\)
\(x^2+2x+1=\left(x+1\right)^2\)
b) \(x^2+y^2+2xy=\left(x+y\right)^2\)
c) \(9x^2+12x+4=\left(3x+2\right)^2\)
d) \(-4x^2-9-12x=-\left(4x^2+12x+9\right)=-\left(2x+3\right)^2\)
CM
22 tháng 5 2019
a) Ta có P = ( 4 x 2 − 1 ) ( 2 x + 1 ) − ( 2 x − 1 ) − ( 4 x 2 − 1 ) ( 2 x + 1 ) ( 2 x − 1 ) = 3 − 4 x 2
b) Ta có Q = 3 x ( x + 3 ) . ( x + 3 ) ( x − 3 ) − x = 9 − 3 x x + 3
PT
1
CM
13 tháng 10 2019
Xét phương trình hoành độ giao điểm 4 x 2 = 12 x – 9 ↔ 4 x 2 − 12 x + 9 có ∆’ = 0 nên phương trình có nghiệm kép hay đường thẳng tiếp xúc parabol tại một điểm.
Đáp án: B
AD
1
29 tháng 10 2023
a:
ĐKXĐ: \(x^2+3x>=0\)
=>x(x+3)>=0
=>\(\left[{}\begin{matrix}x>=0\\x< =-3\end{matrix}\right.\)
\(\sqrt{16}-\sqrt{x^2+3x}=0\)
=>\(\sqrt{x^2+3x}=\sqrt{16}\)
=>x^2+3x=16
=>x^2+3x-16=0
\(\text{Δ}=3^2-4\cdot1\cdot\left(-16\right)=9+64=73>0\)
Do đó: Phương trình có 2 nghiệm phân biệt là:
\(\left\{{}\begin{matrix}x_1=\dfrac{-3-\sqrt{73}}{2}\\x_2=\dfrac{-3+\sqrt{73}}{2}\end{matrix}\right.\)
b:
ĐKXĐ: \(x\in R\)
\(3x-1-\sqrt{4x^2-12x+9}=0\)
=>\(\sqrt{\left(2x-3\right)^2}=3x-1\)
=>\(\left\{{}\begin{matrix}3x-1>=0\\\left(3x-1\right)^2=\left(2x-3\right)^2\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(3x-1-2x+3\right)\left(3x-1+2x-3\right)=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}x>=\dfrac{1}{3}\\\left(x+2\right)\left(5x-4\right)=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-2\left(loại\right)\\x=\dfrac{4}{5}\left(nhận\right)\end{matrix}\right.\)
c:
ĐKXĐ: \(\left\{{}\begin{matrix}x^2-6x+8>=0\\2x^2-10x+11>=0\end{matrix}\right.\)
=>\(\left\{{}\begin{matrix}\left[{}\begin{matrix}x>=4\\x< =2\end{matrix}\right.\\\left[{}\begin{matrix}x< =\dfrac{5-\sqrt{3}}{2}\\x>=\dfrac{5+\sqrt{3}}{2}\end{matrix}\right.\end{matrix}\right.\)
=>\(\left[{}\begin{matrix}x< =\dfrac{5-\sqrt{3}}{2}\\x>=4\end{matrix}\right.\)
\(\sqrt{2x^2-10x+11}=\sqrt{x^2-6x+8}\)
\(\Leftrightarrow2x^2-10x+11=x^2-6x+8\)
=>\(x^2-4x+3=0\)
=>(x-1)(x-3)=0
=>x=3(loại) hoặc x=1(nhận)
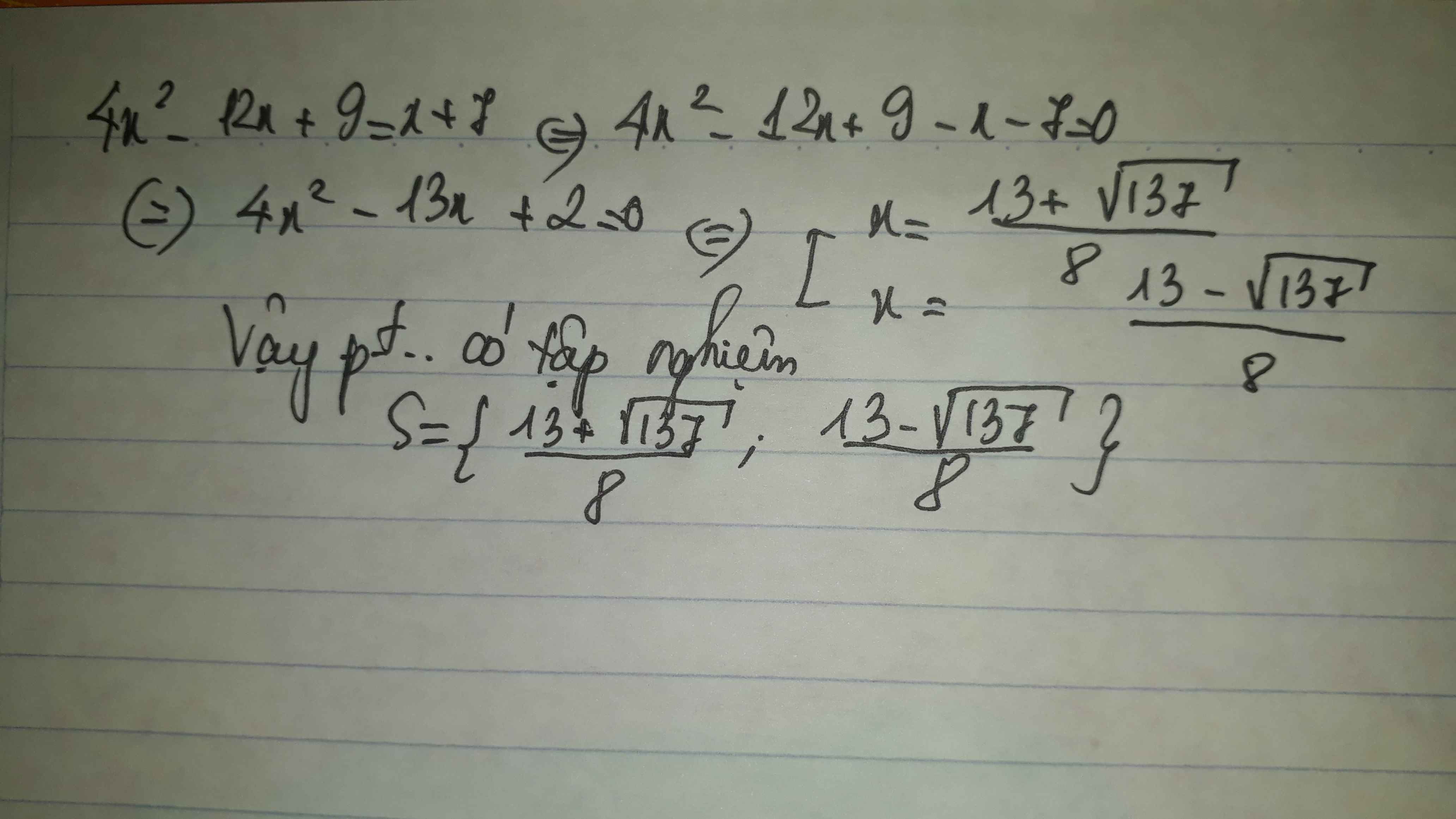
\(=\left(2x-3\right)^2\)
\(\left(2x-3\right)^2\)