60+39=
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
QA
0
AH
Akai Haruma
Giáo viên
17 tháng 2 2021
Lời giải:
$\overrightarrow{AB}\parallel \overrightarrow{C'D'}$ và $|\overrightarrow{AB}|=|\overrightarrow{C'D'}|=a$ nên:
$\overrightarrow{AB}.\overrightarrow{C'D'}=a^2$
PT
1
T
0
NV
Nguyễn Việt Lâm
Giáo viên
28 tháng 1 2021
Do tất cả các cạnh bằng a nên các mặt bên đều là hình thoi.
Mà \(\widehat{BAA'}=\widehat{BAD}=\widehat{DAA'}=60^0\Rightarrow A'B=A'D=AA'=BD=a\)
\(\Rightarrow\) Hình chiếu vuông góc H của A' lên (ABCD) là tâm tam giác đều ABD
\(AH=\dfrac{2}{3}.\dfrac{a\sqrt{3}}{2}=\dfrac{a\sqrt{3}}{3}\) ; \(AC=a\sqrt{3}\)
\(cos\widehat{A'AC}=\dfrac{AH}{AA'}=\dfrac{\sqrt{3}}{3}\Rightarrow cos\widehat{ACC'}=-\dfrac{\sqrt{3}}{3}\)
Áp dụng định lý hàm cos cho tam giác ACC':
\(AC'=\sqrt{AC^2+C'C^2-2AC.C'C.cos\widehat{ACC'}}=a\sqrt{6}\)
TD
3
29 tháng 3 2021
a) trên nữa mp bờ chứa tia ox ta có xot<xoy(30<60)
⇒ot nằm giữa 2 tia còn lại
⇒ xot + toy = xoy
30 độ + toy = 60 độ
toy = 60 độ - 30 độ = 30 độ
b) vì ox' và ox 2 là tia đối
⇒ tia x'oy và xoy là 2 góc kề bù
⇒ x'oy + xoy = 180
x'oy + 60 độ = 180 độ
x'oy = 180 độ - 60 độ = 120 độ
vì oy và oy' là 2 tia đối nhau
⇒ x'oy và x'oy' là 2 góc kề bù
⇒ x'oy + x'oy' = 180 độ
120 độ + x'oy' = 180 độ
x'oy' = 180 độ = 120 độ = 60 độ
vậy x'oy' = 60 độ
29 tháng 3 2021
Ta có: \(\widehat{xOy}=\widehat{x'Oy'}\)(Hai góc đối đỉnh)
mà \(\widehat{xOy}=60^0\)
nên \(\widehat{x'Oy'}=60^0\)
Vậy: \(\widehat{x'Oy'}=60^0\)
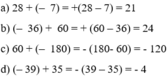
60+39=99
60+39=99
tick nha