Tìm số x thỏa mãn x : 2 5 - 1 2 5 = 1
A. x = 1
B. x = -1
C. x = 5 2
D. x = - 5 2
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

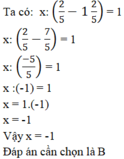

a, \(x\in\left\{-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}\)
Tổng các x thoả mãn: (-5+5)+(-4+4)+(-3+3)+(-2+2)+(-1+1)+0=0+0+0+0+0+0=0
b, \(x\in\left\{-3;-2;-1;0;1;2\right\}\)
Tổng các x thoả mãn: (-2+2) + (-1+1) + 0 + (-3) = 0 + 0 + 0 + (-3) = -3
c, \(x\in\left\{-1;0;1;2;3;4\right\}\)
Tổng các x thoả mãn: (-1+1) + 0 + 2 + 3 + 4 = 9
Tương tự cháu làm các câu d,e,f rồi gửi lên lại thầy check cho hí
\(\text{a) -5 ≤ x < 6 }\)
\(x\in\left\{-5;-4;-3;-2;-1;0;1;2;3;4;5\right\}\)
\(\text{b) -4 < x < 3}\)
\(x\in\left\{-3;-2;-1;0;1;2\right\}\)
\(\text{c) -1 ≤ x ≤ 4}\)
\(x\in\left\{-1;0;1;2;3;4\right\}\)
\(\text{d) -5 < x < 2}\)
\(x\in\left\{-4;-3;-2;-1;0;1\right\}\)
\(\text{e) -5 < x < 5 }\)
\(x\in\left\{-4;-3;-2;-1;0;1;2;3;4\right\}\)
\(\text{f) -6 < x ≤ 4}\)
\(x\in\left\{-5;-4;-3;-2;-1;0;1;2;3;4\right\}\)

Câu 1 .
\(\left|x^2+|x+1|\right|=x^2+5\)
\(Đkxđ:x^2+5\ge0\)
\(\Leftrightarrow x^2\ge-5,\forall x\) ( với mọi x , vì bất cứ số nào bình phương cũng lớn hơn hoặc bằng - 5 )
\(\Leftrightarrow\hept{\begin{cases}x^2+\left|x+1\right|=x^2+5\\x^2+\left|x+1\right|=-x^2-5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}\left|x+1\right|=5\\\left|x+1\right|=-2x^2-5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x+1=5;x+1=-5\\x+1=-2x^2-5;x+1=2x^2+5\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=4;x=-6\\2x^2+x+1=0;-2x^2+x-4=0\end{cases}}\)
\(\Leftrightarrow\hept{\begin{cases}x=4;x=-6\\2x^2+x+1=0\left(VN\right);-2x^2+x-4=0\left(VN\right)\end{cases}}\) ( VN là vô nghiệm nha )
Vậy : x = 4 hoặc x = -6

Bài 4:
\(\left|x+1\right|+\left|2x-3\right|=x-2\)
\(\Leftrightarrow x-2=\left|x+1\right|+\left|2x-3\right|\ge0\)
\(\Leftrightarrow x\ge2\)
\(\Leftrightarrow x+1>0\Leftrightarrow\left|x+1\right|=x+1\)
\(\Leftrightarrow2x-3>0\Leftrightarrow\left|2x-3\right|=2x-3\)
Lúc đó:
\(x+1+2x-3=x-2\)
\(\Leftrightarrow3x-2=x-2\Leftrightarrow x=0\)(Vô lý)
Bài 5:
\(\left|x-1\right|+\left|x-2\right|+\left|x-3\right|=5\)
Trường hợp 1: \(x\ge3\)
\(\left|x-1\right|=x-1\)
\(\left|x-2\right|=x-2\)
\(\left|x-3\right|=x-3\)
Lúc đó:
\(x-1+x-2+x-3=5\)
\(\Leftrightarrow3x-6=5\Leftrightarrow x=\frac{11}{3}\)(Thỏa mãn)
Trường hợp 2: \(2\le x\le3\)
\(\left|x-1\right|=x-1\)
\(\left|x-2\right|=x-2\)
\(\left|x-3\right|=3-x\)
Lúc đó:
\(x-1+x-2+3-x=5\)
\(\Leftrightarrow2x=5\Leftrightarrow x=\frac{5}{2}\)(Thỏa mãn)
Trường hợp 3:\(1\le x\le2\)
\(\left|x-1\right|x=x-1\)
\(\left|x-2\right|=2-x\)
\(\left|x-3\right|=3-x\)
Lúc đó:
\(x-1+2-x+3-x=5\)
\(\Leftrightarrow4-x=5\Leftrightarrow x=\left(-1\right)\)(Loại)
Trường hợp 4: \(x< 1\)
\(\left|x-1\right|=1-x\)
\(\left|x-2\right|=2-x\)
\(\left|x-3\right|=3-x\)
Lúc đó:
\(1-x+2-x+3-x=5\)
\(\Leftrightarrow6-3x=5\Leftrightarrow x=\frac{1}{3}\)(Thỏa mãn)