Các mặt bên của hình lăng trụ đứng là
A. Các hình bình hành
B. Các hình thang cân
C. Các hình chữ nhật
D. Các hình vuông
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
A
4 tháng 5 2023
Phát biểu nào sau đây là đúng?
A. Các mặt bên của hình lăng trụ đứng là hình chữ nhật
B. Các mặt bên của hình lăng trụ đứng là hình thang cân
C. Các mặt đáy của hình lăng truh đứng là các hình chữ nhật
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác
4 tháng 5 2023
Phát biểu nào sau đây là đúng?
A. Các mặt bên của hình lăng trụ đứng là hình chữ nhật
B. Các mặt bên của hình lăng trụ đứng là hình thang cân
C. Các mặt đáy của hình lăng truh đứng là các hình chữ nhật
D. Các mặt đáy của hình lăng trụ đứng là các hình tam giác
QT
Quoc Tran Anh Le
Giáo viên
22 tháng 9 2023
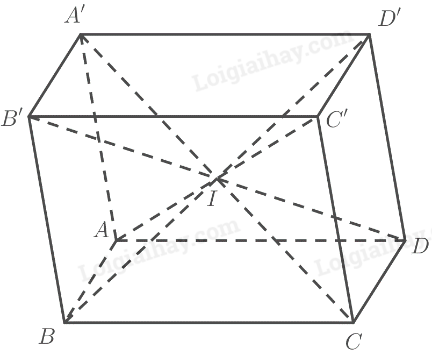
a) Vì \(ABCD.A'B'C'D'\) là hình lăng trụ nên có:
‒ Hai đáy \(ABCD\) và \(A'B'C'D'\) bằng nhau và là hình bình hành.
‒ Các mặt bên \(AA'B'B,AA'D'D,BB'C'C,CC'D'D\) là các hình bình hành.
b) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {AA'C'C} \right) \cap \left( {ABC{\rm{D}}} \right) = AC\\\left( {AA'C'C} \right) \cap \left( {A'B'C'D'} \right) = A'C'\end{array} \right\} \Rightarrow AC\parallel A'C'\)
Mà \(AA'\) và \(CC'\) là các cạnh bên của hình lăng trụ nên \(AA'\parallel CC'\)
Vậy \(AA'C'C\) là hình bình hành.
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {BB'D'D} \right) \cap \left( {ABC{\rm{D}}} \right) = B{\rm{D}}\\\left( {BB'D'D} \right) \cap \left( {A'B'C'D'} \right) = B'D'\end{array} \right\} \Rightarrow B{\rm{D}}\parallel B'D'\)
Mà \(BB'\) và \(DD'\) là các cạnh bên của hình lăng trụ nên \(BB'\parallel DD'\)
Vậy \(BB'D'D\) là hình bình hành.
c) Ta có:
\(\left. \begin{array}{l}\left( {ABC{\rm{D}}} \right)\parallel \left( {A'B'C'D'} \right)\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {ABC{\rm{D}}} \right) = C{\rm{D}}\\\left( {A'B'C{\rm{D}}} \right) \cap \left( {A'B'C'D'} \right) = A'B'\end{array} \right\} \Rightarrow C{\rm{D}}\parallel A'B'\left( 1 \right)\)
\(ABC{\rm{D}}\) là hình bình hành nên \(AB = CD\)
\(AA'B'B\) là hình bình hành nên \(AB = A'B'\)
Vậy \(A'B' = CD\left( 2 \right)\)
Từ (1) và (2) suy ra \(A'B'C{\rm{D}}\) là hình bình hành
\( \Rightarrow A'C,B'D\) cắt nhau tại trung điểm của mỗi đường.
Chứng minh tương tự ta có:
+ \(ABC'D'\) là hình bình hành nên \(AC',B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
+ \(A'BCD'\) là hình bình hành nên \(A'C,B{\rm{D}}'\) cắt nhau tại trung điểm của mỗi đường
Do đó bốn đoạn thẳng \(A'C,AC',B'D,BD\) có cùng trung điểm.
HQ
Hà Quang Minh
Giáo viên
22 tháng 9 2023
\(ABB'A'\) là hình chữ nhật \( \Rightarrow AA' \bot AB\)
\(ACC'A'\) là hình chữ nhật \( \Rightarrow AA' \bot AC\)
\(\left. \begin{array}{l} \Rightarrow AA' \bot \left( {ABC} \right)\\AA'\parallel BB'\parallel CC'\end{array} \right\} \Rightarrow BB' \bot \left( {ABC} \right),CC' \bot \left( {ABC} \right)\)
Vậy các cạnh bên của lăng trụ đó vuông góc với các mặt đáy.
CM
21 tháng 6 2017
Tương tự 2A
a) (i) Có 8 đỉnh, 12 cạnh và 6 mặt.
(ii) Hình lăng trụ đứng ABDC.A'B'D'C' không là hình hộp chữ nhật vì các đáy không phải là hình chữ nhật.
b) (BCC'B') ^ (ABDC)
CM
16 tháng 7 2019
Tương tự 3A.
a) Chiều cao lăng trụ là 4cm.
b) SABB'A'=12cm2 và S2đáy = 9cm2
HQ
Hà Quang Minh
Giáo viên
19 tháng 9 2023
Mặt bên tương ứng với hình chữ nhật như sau
(1)-ACC’A’
(2)- BCC’B’
(3)-ABB’A’
VN
Võ Ngọc Phương
VIP
28 tháng 12 2023
Ta có:
Hình chữ nhật có 2 trục đối xứng.
Hình thang cân có 1 trục đối xứng.
Hình bình hành không có trục đối xứng.
Hình thoi có 2 trục đối xứng.
Hình tam giác đều có 3 trục đối xứng.
Hình vuông có 4 trục đối xứng.
\(\Rightarrow\) Chọn đáp án C.
\(#Nulc`\)
Hình lăng trụ đứng có hai đáy là những đa giác, các mặt bên là những hình chữ nhật.
Đáp án cần chọn là: C