Để hệ phương trình x + y = S x y = P có nghiệm, điều kiện cần và đủ là:
A. S 2 – P < 0
B. S 2 – P ≥ 0
C. S 2 – 4 P < 0
D. S 2 – 4 P ≥ 0
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

- Ta có: x, y là nghiệm phương trình X 2 - S X + P = 0
- Hệ phương trình có nghiệm khi ∆ = S 2 - 4 P ≥ 0
Đáp án cần chọn là: D

Đáp án D
Hệ phương trình đối xứng loại 1 với cách đặt 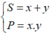 điều kiện
S
2
≥
4
P
⇔
S
2
-
4
P
≥
0
điều kiện
S
2
≥
4
P
⇔
S
2
-
4
P
≥
0


Với m = -2 thì (*) trở thành: 0x = 0 ( luôn đúng với mọi x). Khi đó, hệ phương trình có vô số nghiệm
Với m= -4 thì (*) trở thành: 0x = -10 ( vô lí) do đó hệ phương trình đã cho có vô nghiệm
Với m ≠ 2 ; m ≠ 4 thì (*) có nghiệm duy nhất nên hệ phương trình đã cho có nghiệm duy nhất.
Vậy điều kiện cần và đủ để hệ phương trình có nghiệm là m ≠ 2
Chọn A

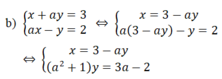
Do a 2 + 1 ≠ 0 ∀ x nên hệ phương trình trở thành:
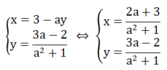
Khi đó:
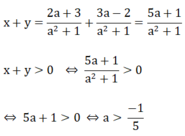
Vậy với a > (-1)/5 thì hệ phương trình có nghiệm duy nhất (x; y) thỏa mãn x+y >0

Ta có x + 2 y = 2 m x − y = m
⇔ x = 2 − 2 y m 2 − 2 y − y = m ⇔ x = 2 − 2 y 2 m + 1 y = m
Để phương trình có nghiệm duy nhất thì m ≠ - 1 2
Suy ra y = m 2 m + 1 ⇒ x = 2 − 2. m 2 m + 1 ⇒ x = 2 m + 2 2 m + 1
Vậy hệ có nghiệm duy nhất x = 2 m + 2 2 m + 1 y = m 2 m + 1
Để x > 1 y > 0
⇔ 2 m + 2 2 m + 1 > 1 m 2 m + 1 > 0 ⇔ 1 2 m + 1 > 0 m 2 m + 1 > 0 ⇔ 2 m + 1 > 0 m > 0 ⇔ m > − 1 2 m > 0 ⇒ m > 0
Kết hợp điều kiện m ≠ - 1 2 ta có m > 0
Đáp án: A
Đáp án: D