Cho parabol (P): y = 1 4 x 2 và đường thẳng d: y = 11 8 x - 3 2 . Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm...

PT

Pham Trong Bach

25 tháng 8 2018

Cho parabol (P): y = 1 4 x 2 và đường thẳng d: y = 11 8 x - 3 2 . Gọi A, B là các giao điểm của (P) và d. Tìm tọa độ điểm C trên trục tung cho CA + CB có giá trị nhỏ nhất. A. C 3 2 ; 0 B. C 0 ; 3 2 C. C 1 2 ; 0 D. C 0 ; - 3 2 ...

Đọc tiếp

#Toán lớp 9

1

CM

Cao Minh Tâm

25 tháng 8 2018

Đáp án B

Đúng(0)

B

binn2011

29 tháng 1 2020 - olm

Trong mặt phẳng tọa độ Oxy, cho parabol (P) : y = x^2 và đường thẳng (d) : y = -x + 2

a, Tìm tọa độ giao điểm của (P) và (d)

b, Gọi A,B là 2 giao điểm của (P) và (d). Tính diện tích tam giác OAB

#Toán lớp 9

0

NB

Nhi Bảo

26 tháng 3 2023

trên mặt phẳng tọa độ Oxy cho đường thẳng (d):y=-x+2 và Parabol (P):y=x² a)vẽ đồ thị của (d) và (P) trên cùng 1 hệ trục tọa độ b)Tìm tọa độ giao điểm của (P) và (d) (bằng phép tính) c) gọi A và B là 2 giao điểm của (d ) và (P). Tính diện tích tam giác OAB

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

26 tháng 3 2023

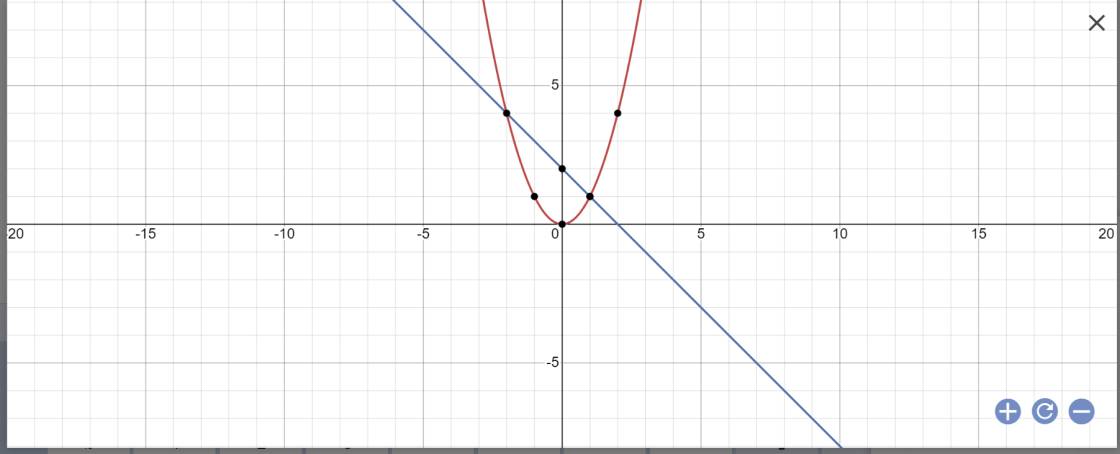
a loading...

b:

PTHĐGĐ là:

x^2+x-2=0

=>(x+2)(x-1)=0

=>x=-2 hoặc x=1

=>y=4 hoặc y=1

Đúng(0)

LH

Lê Huyền

26 tháng 3 2022

Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y=x^2 và đường thẳng (d): y=-x+2
a, Vẽ đồ thị của 2 hàm số trên cùng 1 hệ trục tọa độ
b, Tìm tọa độ giao điểm của (P) và (d)
c, Gọi A,B là 2 giao điểm của (P) và (d). Tính diện tích tam giác OAB

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

14 tháng 7 2023

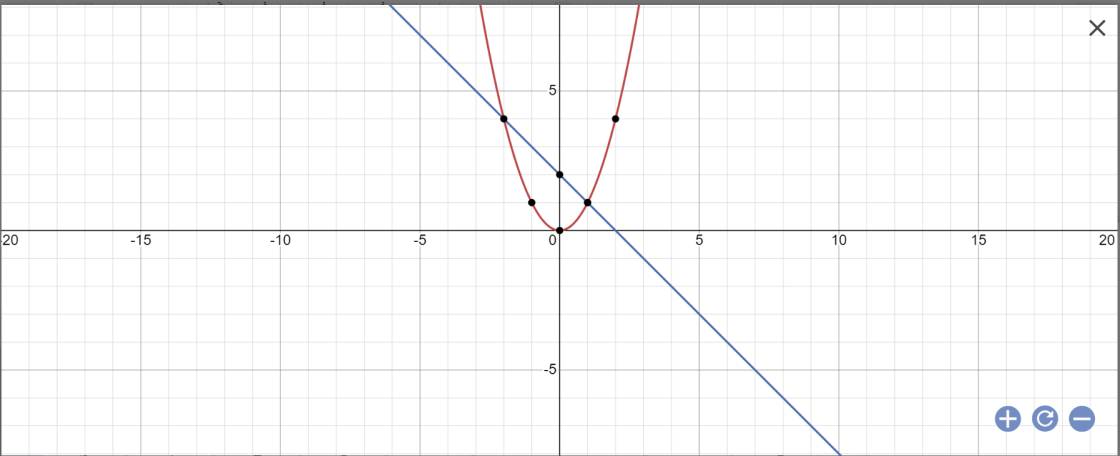
a: loading...

b: PTHĐGĐ là:

x^2+x-2=0

=>(x+2)(x-1)=0

=>x=-2 hoặc x=1

=>y=4 hoặc y=1

Đúng(0)

HT

Hoàng Thành Long

9 tháng 6 2015 - olm

Trên mặt phẳng tọa độ Oxy cho đường thẳng (d) : y = - x + 6 và parabol (P): y = x².

a, Tìm tọa độ các giao điểm của (d) và (P).

b, Gọi A, B là giao điểm của (d) và (P). Tính diện tích tam giác OAB.

#Toán lớp 9

2

NT

ngô thị loan

10 tháng 6 2015

câu a: phương trình hoành độ giao điểm x^2= -x+6 <=> x^2 +x-6=0 <=> x=2 và x=-3

toạ độ các giao điểm là A(2;4) và B(-3;9)

câu b: bạn phải vẽ hình ra ta sẽ thấy tam giác OAB là tam giác vuông với 2 cạnh OA và OB là 2 cạnh góc vuông, dựa vào hình vẽ sẽ tính được

tính OA=$\sqrt{\left(2^2+4^2\right)}$=$\sqrt{20}$ và OB=$\sqrt{\left(\left(-3\right)^2+9^2\right)}$= $\sqrt{90}$ sau đó tính diện tích tam giác OAB

S=$\frac{1}{2}OA\cdot OB=\frac{1}{2}\sqrt{20}\cdot\sqrt{90}$=$3\sqrt{50}$

Đúng(0)

CC

Cao Chi Hieu

22 tháng 4 2018

ngô thị loan tại sao lại có thể nhìn hình để kết luận là tam giác vuông liền được ? mình vẽ đồ thị ra thi có phải tam giác vuông đâu, dùng Pytago thử lại cũng sai ??

Đúng(1)

NH

Nguyễn Hoàng Minh

26 tháng 2 2022

Trên mặt phẳng tọa độ đạt GTNN $Oxy$, cho parabol $(P):y=\frac{1}{2}x^2$ và đường thẳng $(d):y=\frac{1}{2}x+3.$ Gọi $A(x_A;y_A),B(x_B;y_B)$ (với $x_A<x_B$) là các giao điểm của $(P)$ và $(d),C(x_C;y_C)$ là điểm thuộc $(P)$ sao cho $x_A<x_C<x_B$. Tìm GTLN của $S_{ABC}$ ** Làm theo cách lớp 9, ko xài CT tính k/c từ 1 điểm đến 1 đường...

Đọc tiếp

#Toán lớp 9

0

ND

Nguyen Dang Hai Dang

28 tháng 8 2023 - olm

Trong mặt phẳng tọa độ Oxy, cho Parabol (P): y = x2 và đường thẳng (d): y = -x + 2 a) Tìm tọa độ giao điểm của (P) và (Q) b) Gọi A, B là hai giao điểm của (P) và (Q). Tính diện tích tam giác...

Đọc tiếp

#Toán lớp 9

2

ND

Nguyễn Đức Trí

VIP

28 tháng 8 2023

$\left\{{}\begin{matrix}\left(P\right):y=x^2\\\left(d\right):y=-x+2\end{matrix}\right.$

a) Tọa độ giao điểm của (P) và (Q) là nghiệm của hệ phương trình

$\left\{{}\begin{matrix}y=x^2\\y=-x+2\end{matrix}\right.$ $\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2=-x+2\end{matrix}\right.$ $\Leftrightarrow\left\{{}\begin{matrix}y=x^2\\x^2+x-2=0\left(1\right)\end{matrix}\right.$

$pt\left(1\right)\Leftrightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.$ $\left(a+b+c=1+1-2=0\right)$

$hpt\Leftrightarrow\left[{}\begin{matrix}\left\{{}\begin{matrix}x=1\\y=1\end{matrix}\right.\\\left\{{}\begin{matrix}x=-2\\y=4\end{matrix}\right.\end{matrix}\right.$

Vậy tọa độ giao điểm của (P) và (Q) là $A\left(1;1\right)\&B\left(-2;4\right)$

Đúng(1)

XO

Xyz OLM

28 tháng 8 2023

a) Phương trình hoành độ giao điểm :

x² = - x + 2

<=> (x - 1)(x + 2) = 0

<=> $\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.$

Với x = 1 ta được y = 1

Với x = -2 ta được y = 4

Vậy tọa độ giao điểm là A(1; 1) ; B(-2;4)

b) Gọi C(-2 ; 0) ; D(1;0)

ta được $S_{AOB}=S_{ABCD}-S_{BOC}-S_{AOD}$

$=\dfrac{\left(BC+AD\right).CD}{2}-\dfrac{BC.CO}{2}-\dfrac{AD.DO}{2}$

$=\dfrac{\left(4+1\right).3}{2}+\dfrac{4.2}{2}+\dfrac{1.1}{2}=12$ (đvdt)

Đúng(1)

NC

Nguyễn Châu Mỹ Linh

5 tháng 5 2021

Trong mặt phẳng tọa độ Oxy, cho parabol (P): y=x2 và đường thẳng (d): y=2(m-1)x+5-2m (m là tham số)

a) Vẽ đồ thị parabol (P).

b) Biết đường thẳng (d) luôn cắt parabol (P) tại hai điểm phân biệt. Gọi hoành độ giao điểm của đường thẳng (d) và parabol (P) là x1, x2. Tìm m để x+x=6

#Toán lớp 9

1

NL

Nguyễn Lê Phước Thịnh

5 tháng 5 2021

b) Phương trình hoành độ giao điểm của (P) và (d) là:

$x^2=2\left(m-1\right)x+5-2m$

$\Leftrightarrow x^2-2\left(m-1\right)x-5+2m=0$

Áp dụng hệ thức Vi-et, ta được:

$x_1+x_2=2\left(m-1\right)$

Ta có: $x_1+x_2=6$

$\Leftrightarrow2\left(m-1\right)=6$

$\Leftrightarrow m-1=3$

hay m=4

Vậy: m=4

Đúng(3)

H

Haley

28 tháng 1 2018 - olm

Giúp em với ạ !!

Cho parabol P y=x^2 và đường thẳng (d): y=2x+3. Gọi A và B là hai giao điểm của P và (d). Tọa độ giao điểm của AB là ?

#Toán lớp 9

1

H

Haley

28 tháng 1 2018

Tìm tọa độ trung điểm của AB là C (a;b) ạ

Đúng(0)

KK

Kim Khánh Linh

14 tháng 5 2021 - olm

Trong mặt phẳng tọa độ $O x y$ cho parabol $(P): y=x^{2}$ và đường thẳng $(d): y=(2 m-1) x-m^{2}+2$ ($m$ là tham số)

a) Tìm tọa độ giao điểm của đường thẳng $(d)$ và parabol $(P)$ khi $m=2$.

b) Tìm các giá trị của tham số $m$ để $(d)$ cắt $(P)$ tại $2$ điểm phân biệt có hoành độ $x_{1}, x_{2}$ thỏa mãn $x_{1}-3 x_{2}=7$.

#Toán lớp 9

1

LT

Lê Tài Bảo Châu

15 tháng 5 2021

a) Xét phương trình hoành độ giao điểm chung của (d) và (P) :

$x^2=\left(2m-1\right)x-m^2+2$

$\Leftrightarrow x^2-\left(2m-1\right)x+m^2-2=0\left(1\right)$

Thay m=2 vào pt (1) ta được:

$x^2-3x+2=0$

$\Leftrightarrow\orbr{\begin{cases}x=1\Rightarrow y=1\\x=2\Rightarrow y=4\end{cases}}$

Tọa độ giao điểm của (d) và (P) khi m=2 là $A\left(1;1\right);B\left(2;4\right)$

b) $\Delta_{\left(1\right)}=\left(2m-1\right)^2-4m^2+8$

$=4m^2-4m+1-4m^2+8$

$=9-4m$

Để pt (1) có 2 n ghiệm pb $\Leftrightarrow9-4m>0\Leftrightarrow m< \frac{9}{4}$

Theo hệ thức Vi-et ta có:

$\hept{\begin{cases}x_1+x_2=2m-1\\x_1.x_2=m^2-2\left(1\right)\end{cases}}$

Ta có: $\hept{\begin{cases}x_1+x_2=2m-1\\x_1-3x_2=7\end{cases}}$

$\Leftrightarrow\hept{\begin{cases}3x_1+3x_2=6m-3\\x_1-3x_2=7\end{cases}}$

$\Leftrightarrow\hept{\begin{cases}x_1=\frac{3m+2}{2}\\x_2=\frac{m-4}{2}\end{cases}\left(3\right)}$

Thay (3) vào (2) ta được:

$\frac{3m+2}{2}.\frac{m-4}{2}=m^2-2$

$\Leftrightarrow\frac{3m^2-10m-8}{4}=m^2-2$

$\Rightarrow3m^2-10m-8=4m^2-8$

$\Leftrightarrow m^2+10m=0$

$\Leftrightarrow\orbr{\begin{cases}m=0\\m=-10\end{cases}\left(tm\right)}$

Vậy ...

Đúng(0)

TT

Thầy Tùng Dương

VIP

14 tháng 5 2021 - olm

Trong mặt phẳng tọa độ $O x y$ cho Parabol $(P): y=x^{2}$ và đường thẳng $(d): y=m x+3$ ($m$ là tham số)
a) Tìm tọa độ giao điểm của $(d)$ và $(P)$ khi $m=2$.
b) Tìm $m$ để đường thẳng $(d)$ cắt parabol $(P)$ tại hai điểm phân biệt có hoành độ $x_{1} ; x_{2}$ thỏa mãn $\frac{1}{x_{1}}+\frac{1}{x_{2}}=\frac{3}{2}$.

#Toán lớp 9

1

NM

Nguyễn Minh Đăng

14 tháng 5 2021

a) Khi m = 2 thì: $\hept{\begin{cases}y=x^2\\y=2x+3\end{cases}}$

Hoành độ giao điểm (P) và (d) là nghiệm của PT: $x^2=2x+3\Leftrightarrow x^2-2x-3=0\Leftrightarrow\left(x+1\right)\left(x-3\right)=0$

$\Leftrightarrow\orbr{\begin{cases}x+1=0\\x-3=0\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=-1\Rightarrow y=1\\x=3\Rightarrow y=9\end{cases}}$

Vậy tọa độ giao điểm của (P) và (d) là $\left(-1;1\right)$ và $\left(3;9\right)$

b) Hoành độ giao điểm của (P) và (d) là nghiệm của PT:

$x^2=mx+3\Leftrightarrow x^2-mx-3=0$

Vì $ac=1\cdot\left(-3\right)< 0$ => PT luôn có 2 nghiệm phân biệt

Theo hệ thức viet ta có: $\hept{\begin{cases}x_1+x_2=m\\x_1x_2=-3\end{cases}}$

Mà $\frac{1}{x_1}+\frac{1}{x_2}=\frac{3}{2}\Leftrightarrow\frac{x_1+x_2}{x_1x_2}=\frac{3}{2}\Leftrightarrow\frac{-m}{3}=\frac{3}{2}\Rightarrow m=-\frac{9}{2}$

Vậy $m=-\frac{9}{2}$

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP