Cho hàm số f(x) xác định trên R có đồ thị như hình vẽ.
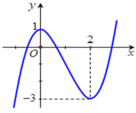
Phương trình 2 f x - 1 = 0 có bao nhiêu nghiệm?
A. 1
B. 3
C. 2
D. 4
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

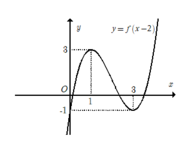
+ Trước tiên tịnh tiến đồ thị sang phải 2 đơn vị để được đồ thị hàm số y= f(x-2) .
Tiếp theo giữ phần đồ thị phía bên phải đường thẳng x= 2, xóa bỏ phần đồ thị phía bên trái đường thẳng x= 2.
Cuối cùng lấy đối xứng phần đồ thị vừa giữ lại ở trên qua đường thẳng x= 2. Ta được toàn bộ phần đồ thị của hàm số
y = f(|x-2|) (hĩnh vẽ bên dưới)
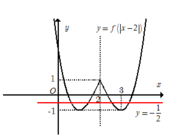
Dựa vào đồ thị hàm số y = f(|x -2|) , ta thấy đường thẳng y= -1/2 cắt đồ thị hàm số y = f(|x-2|) tại 4 điểm phân biệt khi và chỉ khi phương trình f(|x-2|) = -1/2 có 4 nghiệm phân biệt.
Chọn D.

Đáp án là D
Từ đồ thị f ’(x) ta lập được BBT của f(x)
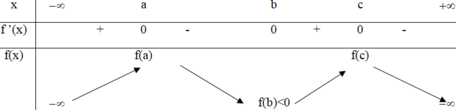
=> Có 4 nghiệm là nhiều nhất
Phương trình đã cho tương đương f x = 1 2
Số nghiệm của phương trình là số giao điểm của đồ thị hàm số y = f x và đường thẳng y = 1 2
Quan sát đồ thị hàm số ta thấy đường thẳng y = 1 2 cắt đồ thị hàm số y = f x tại đúng 3 điểm phân biệt.
Vậy phương trình 2 f x - 1 = 0 có 3 nghiệm phân biệt.
Đáp án cần chọn là: B