Tìm Min,Max: x2+x+1/x2+2x+1
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Không có max
`a)sqrt{x^2-2x+5}`
`=sqrt{x^2-2x+1+4}`
`=sqrt{(x-1)^2+4}`
Vì `(x-1)^2>=0`
`=>(x-1)^2+4>=4`
`=>sqrt{(x-1)^2+4}>=sqrt4=2`
Dấu "=" xảy ra khi `x=1.`
`b)2+sqrt{x^2-4x+5}`
`=2+sqrt{x^2-4x+4+1}`
`=2+sqrt{(x-2)^2+1}`
Vì `(x-2)^2>=0`
`=>(x-2)^2+1>=1`
`=>sqrt{(x-2)^2+1}>=1`
`=>sqrt{(x-2)^2+1}+2>=3`
Dấu "=" xảy ra khi `x=2`

\(A=x^2-2x+50\)
\(A=x^2-2x+1+49\)
\(A=\left(x-1\right)^2+49\ge49\)
Dấu "=" xảy ra khi:
\(x=1\)
\(B=12x-x^2\)
\(B=-x^2+12x\)
\(B=-x^2+12x-36+36\)
\(B=-\left(x^2-12x+36\right)+36\)
\(B=-\left(x-6\right)^2+36\le36\)
Dấu "=" xảy ra khi:
\(x=6\)
\(C=\left(x+1\right)\left(x-2\right)\left(x-3\right)\left(x-6\right)\)
\(C=\left[\left(x+1\right)\left(x-6\right)\right]\left[\left(x-2\right)\left(x-3\right)\right]\)
\(C=\left[x\left(x-6\right)+1\left(x-6\right)\right]\left[x\left(x-3\right)-2\left(x-3\right)\right]\)
\(C=\left(x^2-6x+x-6\right)\left(x^2-3x-2x+6\right)\)
\(C=\left(x^2-5x-6\right)\left(x^2-5x+6\right)\)
\(C=\left(x^2-5x\right)^2-36\ge-36\)
Dấu "=" xảy ra khi:
\(x^2-5x=0\)
\(\Rightarrow x\left(x-5\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x=0\\x=5\end{matrix}\right.\)

B = 2\(x^2\) - 4\(x\) - 8
B = 2(\(x^2\) - 2\(x\) + 4) - 16
B = 2(\(x-2\))2 - 16
Vì (\(x-2\))2 ≥ 0 ∀ \(x\) ⇒ 2(\(x-2\))2 ≥ 0 ∀ \(x\)
⇒ 2(\(x-2\))2 - 16 ≥ -16 ∀ \(x\)
Dấu bằng xảy ra khi (\(x-2\))2 = 0 ⇒ \(x-2=0\) ⇒ \(x=2\)
Vậy Bmin = -16 khi \(x=2\)
Tìm min của C biết:
C = \(x^2\) - 2\(xy\) + 2y2 + 2\(x\) - 10y + 17
C = (\(x^2\) - 2\(xy\) + y2) + 2(\(x\) - y) + y2 - 8y + 16 + 1
C = (\(x\) - y)2 + 2(\(x\) - y) + 1 + (y2 - 8y + 16)
C = (\(x-y+1\))2 + (y - 4)2
Vì (\(x\) - y + 1)2 ≥ 0 ∀ \(x;y\); (y - 4)2 ≥ 0 ∀ y
Dấu bằng xảy ra khi: \(\left\{{}\begin{matrix}x-y+1=0\\y-4=0\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x-y+1=0\\y=4\end{matrix}\right.\)
⇒ \(\left\{{}\begin{matrix}x-4+1=0\\y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=-1+4\\y=4\end{matrix}\right.\) ⇒ \(\left\{{}\begin{matrix}x=3\\y=4\end{matrix}\right.\)
Vậy Cmin = 0 khi (\(x;y\)) = (3; 4)

\(\dfrac{x^2+y^2}{2}\ge xy\Rightarrow-xy\ge-\dfrac{x^2+y^2}{2}\)
\(\Rightarrow4=x^2+y^2-xy\ge x^2+y^2-\dfrac{x^2+y^2}{2}=\dfrac{x^2+y^2}{2}\)
\(\Rightarrow x^2+y^2\le8\)
\(C_{max}=8\) khi \(x=y=\pm2\)
\(x^2+y^2\ge-2xy\Rightarrow-xy\le\dfrac{x^2+y^2}{2}\)
\(4=x^2+y^2-xy\le x^2+y^2+\dfrac{x^2+y^2}{2}=\dfrac{3}{2}\left(x^2+y^2\right)\)
\(\Rightarrow x^2+y^2\ge\dfrac{8}{3}\)
\(C_{min}=\dfrac{8}{3}\) khi \(\left(x;y\right)=\left(-\dfrac{2}{\sqrt{3}};\dfrac{2}{\sqrt{3}}\right);\left(\dfrac{2}{\sqrt{3}};-\dfrac{2}{\sqrt{3}}\right)\)


\(B=2x^2-4x-8=2\left(x^2-2x-4\right)\)
\(=2\left(x^2-2x+1-5\right)\)
\(=2\left[\left(x-1\right)^2-5\right]\)
\(=2\left(x-1\right)^2-10\ge-10\)
Vậy \(B_{min}=-10\Leftrightarrow x-1=0\Leftrightarrow x=1\)
\(F=\left(x+1\right)\left(x+2\right)\left(x+3\right)\left(x+4\right)\)
\(=\left(x+1\right)\left(x+4\right)\left(x+2\right)\left(x+3\right)\)
\(=\left(x^2+5x+4\right)\left(x^2+5x+6\right)\)
Đặt \(x^2+5x+4=t\)
\(\RightarrowĐT=t\left(t+2\right)=t^2+2t+1-1\)
\(=\left(t+1\right)^2-1\ge-1\)
hay \(\left(x^2+5x+5\right)^2-1\ge-1\)
Vậy \(F_{min}=-1\Leftrightarrow x^2+5x+5=0\)
\(\Leftrightarrow x^2+5x+\frac{25}{4}-\frac{5}{4}=0\)
\(\Leftrightarrow\left(x+\frac{5}{2}\right)^2=\frac{5}{4}\)
\(\Leftrightarrow\orbr{\begin{cases}x+\frac{5}{2}=\sqrt{\frac{5}{4}}\\x+\frac{5}{2}=-\sqrt{\frac{5}{4}}\end{cases}}\Leftrightarrow\orbr{\begin{cases}x=\sqrt{\frac{5}{4}}-\frac{5}{2}\\x=-\sqrt{\frac{5}{4}}-\frac{5}{2}\end{cases}}\)
\(G=4x-x^2=-\left(x^2-4x+4-4\right)\)
\(=-\left[\left(x-2\right)^2-4\right]=-\left(x-2\right)^2+4\le4\)
Vậy \(G_{max}=4\Leftrightarrow x-2=0\Leftrightarrow x=2\)
\(H=25-x-5x^2=-5\left(x^2+\frac{x}{5}-5\right)\)
\(=-5\left(x^2+2x.\frac{1}{10}+\frac{1}{100}-\frac{501}{100}\right)\)
\(=-5\left[\left(x+\frac{1}{10}\right)^2-\frac{501}{100}\right]\)
\(=-5\left(x+\frac{1}{10}\right)^2+\frac{101}{20}\le\frac{101}{2}\)
Vậy \(H_{max}=\frac{101}{2}\Leftrightarrow x+\frac{1}{10}=0\Leftrightarrow x=-\frac{1}{10}\)

Do \(x^2+y^2=1\Rightarrow-1\le x;y\le1\Rightarrow\left\{{}\begin{matrix}y+1\ge0\\1-y\ge0\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}y^2\left(y+1\right)\ge0\\y^2\left(1-y\right)\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}y^3\ge-y^2\\y^3\le y^2\end{matrix}\right.\)
Với mọi số thực x ta có:
\(\left\{{}\begin{matrix}\left(x+1\right)^2\ge0\\\left(x-1\right)^2\ge0\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}2x\ge-x^2-1\\2x\le x^2+1\end{matrix}\right.\)
Do đó: \(\left\{{}\begin{matrix}P=2x+y^3\ge-x^2-1-y^2=-2\\P=2x+y^3\le x^2+1+y^2=2\end{matrix}\right.\)
\(P_{min}=-2\) khi \(\left(x;y\right)=\left(-1;0\right)\)
\(P_{max}=2\) khi \(\left(x;y\right)=\left(1;0\right)\)
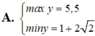
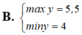
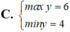
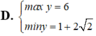
 Đúng thì like giúp mik nha bạn. Thx bạn
Đúng thì like giúp mik nha bạn. Thx bạn