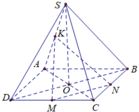
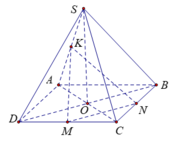
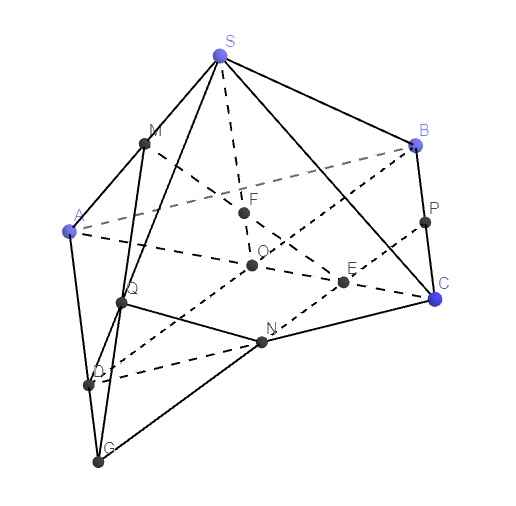
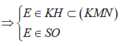Cho hình chóp SABCD có đấy ABCD là hình bình hành tâm O. Gọi M, N, K lần lượt là trung điểm của CB, CD và SO. Tìm giao điểm H của SD và (MNK). Tính \(\frac{HS}{HD}\)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
HT
22 tháng 12 2020
Đề bài sai òi :v Vẽ hình ra đi bạn.
Giờ tui gán MN vô (SBD) thì giao tuyến của (SBD) và (SBC) là SB. Vậy nên SB phải song song với MN. Nhưng ko :) Song song chết liền hà :)
NV
Nguyễn Việt Lâm
Giáo viên
21 tháng 8 2021
Trong mp (ABCD), nối NP kéo dài cắt AD tại G
Trong mp (SAD), nối MG cắt SD tại Q
\(\Rightarrow Q=SD\cap\left(MNP\right)\)
b.
Trong mp (ABCD), gọi E là giao điểm NP và AC
Trong mp (SAC), nối ME cắt SO tại F
\(\Rightarrow F=SO\cap\left(MNP\right)\)
CM
15 tháng 2 2017
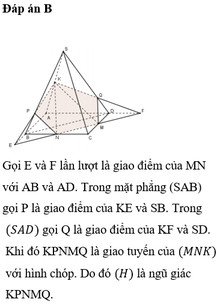
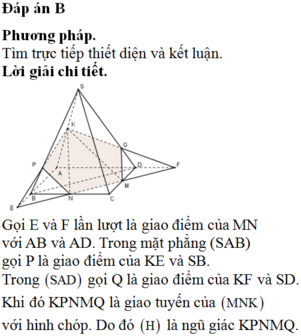
Đáp án B
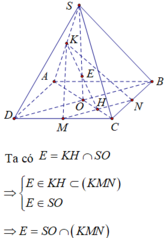
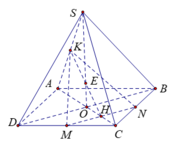
Gọi P = M N ∩ A C ; I = P K ∩ S O
Do M N / / B D nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD, SB lần lượt tại E và F khi đó thiết diện là ngũ giác K E M N F
CM
12 tháng 4 2017
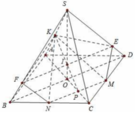
Do MN//BD nên giao tuyến của (MNK) với (SBD) song song với MN. Qua I dựng đường thẳng song song với MN cắt SD,SB lần lượt tại E và F khi đó thiết diện là ngũ giác KEMNF
NV
Nguyễn Việt Lâm
Giáo viên
7 tháng 1 2021
Trong mp (SAD), qua M kẻ đường thẳng song song AD cắt SA tại P
Trong mp (ABCD), qua N kẻ đường thẳng song song AD cắt AB tại Q
\(\Rightarrow PQ\in\left(\alpha\right)\)
Gọi E là giao điểm của AC và NQ
Trong mp (SAC), nối PE cắt SO tại K
\(\Rightarrow K=SO\cap\left(\alpha\right)\)
18 tháng 12 2021
Nối FK kéo dài lần lượt cắt AD và CD tại G và H
Trong mặt phẳng (SAD), nối GE kéo dài cắt SD tại P
Trong mặt phẳng (SCD), nối PH cắt SC tại Q
⇒⇒ Ngũ giác EPQKF là thiết diện của chóp và (EFK)
(Q cũng có thể xác định bằng cách qua E kẻ đường thẳng song song AC cắt SC tại Q. Q đồng thời là trung điểm SC theo t/c đường trung bình
18 tháng 12 2021
Chọn mp ( SAD) chứa SA.
+ (SAD) giao (MNK) = M
- M thuộc SD => M thuộc (SAD).
- M thuộc (MNK)
Trong mp ( ABCD), NK cắt AD tại I.
=> Giao tuyến MI.
Giao tuyến MI cắt SA tại O => O là giao điểm.