Hai tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại I. Đường thẳng qua I và vuông góc với IA cắt OB tại K. Đường thẳng O, vuông góc với OA cắt IB ở C.
a, Chứng minh KC và OI vuông góc với nhau.
b, Biết OA = OB = 9cm, OI = 15cm, tính IA và IK
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
28 tháng 4 2017
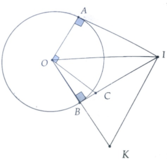
a, Chứng minh C là trực tâm của tam giác OIK. Từ đó suy ra KC ⊥ OI tại H
b, IA=12cm
Chứng minh ΔKOI cân tại K
Đặt KO = KI = x (x>0)
Có I K 2 = I B 2 + B K 2
Hay x 2 = 12 2 + x - 9 2
=> x = 12,5 => IK = 12,5cm
18 tháng 12 2021
b: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuyến
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC
7 tháng 1
a: Xét tứ giác ACBO có \(\widehat{CAO}+\widehat{CBO}=90^0+90^0=180^0\)
nên ACBO là tứ giác nội tiếp
b: Xét tứ giác OIBD có \(\widehat{OID}=\widehat{OBD}=90^0\)
nên OIBD là tứ giác nội tiếp
=>\(\widehat{IBO}=\widehat{IDO}\)
c: Xét tứ giác OAEI có \(\widehat{OAE}+\widehat{OIE}=90^0+90^0=180^0\)
nên OAEI là tứ giác nội tiếp
=>\(\widehat{OEI}=\widehat{OAI}\)
=>\(\widehat{OEI}=\widehat{OAB}=\widehat{OBA}=\widehat{IBO}\)
=>\(\widehat{OEI}=\widehat{ODI}\)
=>ΔOED cân tại O
=>OE=OD
OAK là tam giác cân.
18 tháng 12 2021
1: Xét (O) có
AB là tiếp tuyến
AC là tiếp tuýen
Do đó: AB=AC
hay A nằm trên đường trung trực của BC(1)
Ta có: OB=OC
nên O nằm trên đường trung trực của BC(2)
Từ (1) và (2) suy ra OA⊥BC