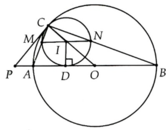
Cho nửa đường tròn tâm O, đường kính AB = 2R và C là một điểm cố định nằm giữa A và B. L hat a y điểm D trên nửa đường tròn (D khác A và B). Qua D vẽ một đường thẳng vuông góc với CD lần lượt cắt các tiếp tuyến Ax, By tại M và N. Gọi P là giao điểm của AD và CM; Q là giao điểm của BD và CN. Chứng minh rằng:
a)Tứ giác CQDP nội tiếp đường tròn.
b) AM.BN=AC.BC
c) Qua D kẻ tiếp tuyến với đường tròn (O) cắt Ax và By lần lượt tại E và F. Tìm giá trị nhỏ nhất của tổng diện tích của hai tam giác AED và BFD.