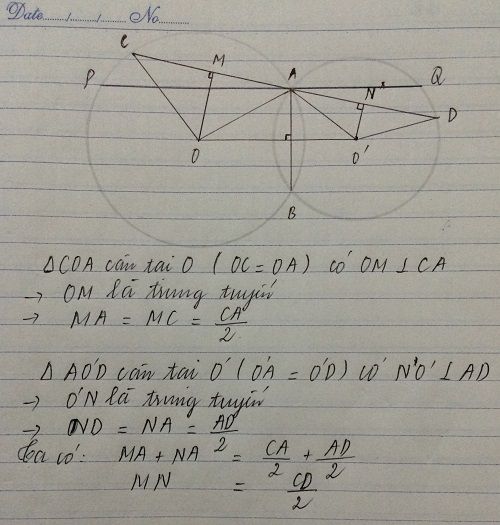Cho 2 đường tròn (O) và (O') cắt nhau ở A và B (O và O' thuộc hai nửa mặt phẳng bờ AB).Qua A kẻ 2 cát tuyến CD và EF (C và E thuộc (O),D và F thuộc (O').Từ B kẻ BH vuông góc với CD,kẻ BK vuông góc với EF.Biết góc CAB bằng góc BAF. a.Chứng minh tam giác BHC bằng tam giác BKE b.So sánh CD và EF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
23 tháng 11 2018
Chắc câu a và câu b dễ rồi
cô chỉ em làm câu c.
Gọi L là trung điểm AP K là trung điểm AQ
=> PQ=2LK=2OO'
Mà CD=2MN , MN<OO,
=> CD<OO'<PQ
VD
13 tháng 7 2018
http://lazi.vn/edu/exercise/cho-o-va-o-cat-nhau-o-a-va-b-o-va-o-thuoc-2-nua-mat-phang-bo-ab-mot-cat-tuyen-ke-qua-a-cat-o-o-c-va-cat-o
AT
4 tháng 7 2021
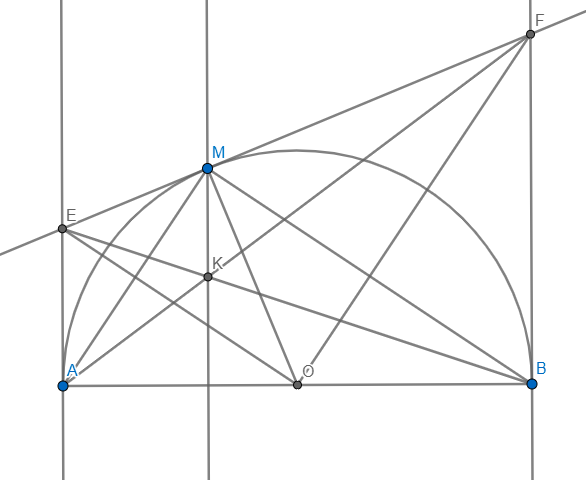
1) Vì EM,EA là tiếp tuyến \(\Rightarrow OE\) là phân giác \(\angle MOA\)
\(\Rightarrow\angle MOE=\dfrac{1}{2}\angle MOA\)
Vì FM,FB là tiếp tuyến \(\Rightarrow OF\) là phân giác \(\angle MOB\)
\(\Rightarrow\angle MOF=\dfrac{1}{2}\angle MOB\)
\(\Rightarrow\angle MOE+\angle MOF=\dfrac{1}{2}\left(\angle MOA+\angle MOB\right)=\dfrac{1}{2}.180=90\)
\(\Rightarrow\angle EOF=90\)
2) Ta có: \(\angle EAO+\angle EMO=90+90=180\Rightarrow AEMO\) nội tiếp
\(\Rightarrow\angle MEO=\angle MAO\)
Vì AB là đường kính \(\Rightarrow\angle AMB=90\)
Xét \(\Delta MAB\) và \(\Delta OEF:\) Ta có: \(\left\{{}\begin{matrix}\angle AMB=\angle EOF\\\angle FEO=\angle MAB\end{matrix}\right.\)
\(\Rightarrow\Delta MAB\sim\Delta OEF\left(g-g\right)\)
Vì \(AE\parallel BF(\bot AB)\) \(\Rightarrow\dfrac{BF}{AE}=\dfrac{FK}{AK}\left(1\right)\)
Vì EM,EA là tiếp tuyến \(\Rightarrow EA=EM\left(2\right)\)
Vì FM,FB là tiếp tuyến \(\Rightarrow FB=FM\left(3\right)\)
Thế (2),(3) vào (1) \(\Rightarrow\dfrac{FM}{EM}=\dfrac{FK}{AK}\Rightarrow\) \(MK\parallel AE\) \(\Rightarrow MK\bot AB\)
