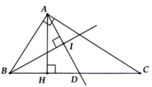
CHO TAM GIÁC ABC VUÔNG TẠI A, KẺ AH VUÔNG GÓC VỚI BC ( H THUỘC BC ). CÁC TIA PHÂN GIÁC GÓC B VÀ GÓC HAC CẮT NHAU TẠI I. CHỨNG MINH RẰNG: GÓC AIB=90 ĐỘ
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
12 tháng 7 2015
TAm giác ABC vuông tại A => ABC + C = 90 độ (1)
TAm giác AHC vuông tại H => HAC + C = 90độ (2)
Từ (1) và (2) => ABC = HAC (3)
Ta có OBA = 1/2 ABC ( BO là phâ n giác ) (4)
Từ (3) và (4) => OBA = 1/2 HAC
OAH = 1/2 HAC ( AO là phân giác)
=>ABO + OAB = 1/2 . HAC + OAH + HAB = 1/2 .HAC + 1/2 .HAC + HAB = HAC + HAB = BAC = 90 độ ( TAm giác ABC vuông tại A )
TAm giác OAB có OBA + OAB = 90 độ => AOB = 90 độ
=> ĐPCM
M
22 tháng 11 2020
Gọi BO giao với AH tại K
Tam giác ABC vuông tại A
\(\Rightarrow\widehat{B}+\widehat{C}=90^o\)(1)
Tam giác AHC có \(\widehat{H}=90^o\)
\(\Rightarrow\widehat{HAC}+\widehat{C}=90^o\)(2)
Từ (1) và (2) => \(\widehat{B}=\widehat{HAC}\)
\(\Rightarrow\widehat{HBO}=\widehat{HAO}\)
lại có \(\hept{\begin{cases}\widehat{HBO}+\widehat{BKH}=90^o\\\widehat{HAO}+\widehat{AKO}=\widehat{HBO}+\widehat{BKH}\end{cases}}\)( vì góc BKH và góc AKO bằng nhau 2 góc đối đỉnh )
\(\Rightarrow\widehat{HAO}+\widehat{AKO}=90^o\)
\(\Rightarrow\widehat{AOB}=90^o\)