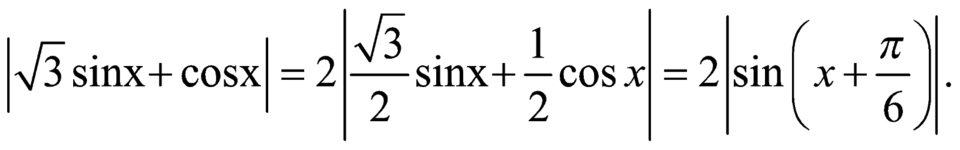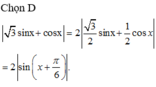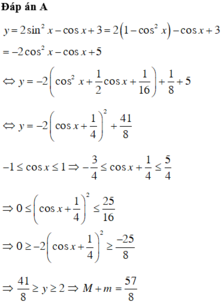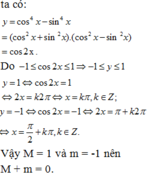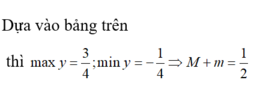K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
26 tháng 9 2018
Ta có: y ' = 2 - ln x ln x x 2
y ' = 0 ⇔ x = 1 x = e 2 y 1 = 0 ; y e 3 = 9 e 3 ; y e 2 = 4 e 2
Suy ra M = 4 e 2 và m = 0
Vậy Q = e 2 M + m = e 2 4 e 2 + 0 = 2
Đáp án B
CM
23 tháng 3 2019
Đáp án C
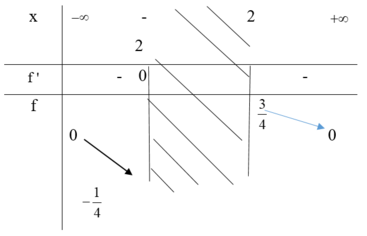
Có y 0 = 0.
Với x ≠ 0 ta có y = x 3 + x 2 + x x 2 x 2 + 1 2 x 2 = x + 1 x + 1 x + 1 x 2 . Đặt x + 1 x = t thì ta có y = f t = t + 1 t 2 .
Thấy v x + 1 x 2 ≥ 4. x . a x = 4 nến t 2 ≥ 4 ⇔ t ∈ − ∞ ; − 2 ∪ 2 ; + ∞ .
Có f ' t = − t 2 − 2 t t 4 . f ' t = 0 ⇔ t = 0 t = − 2
Bảng biến thiên f t với t ∈ − ∞ ; − 2 ∪ 2 ; + ∞ .
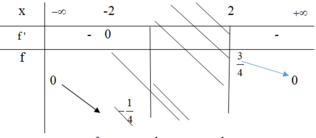
Dựa vào bảng trên thì max y = 3 4 ; min y = − 1 4 ⇒ M + m = 1 2
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 1:
$2xy=(x+y)^2-(x^2+y^2)=4^2-10=6\Rightarrow xy=3$
$M=x^6+y^6=(x^3+y^3)^2-2x^3y^3$
$=[(x+y)^3-3xy(x+y)]^2-2(xy)^3=(4^3-3.3.4)^2-2.3^3=730$
AH
Akai Haruma
Giáo viên
16 tháng 12 2021
Bài 2:
$8x^3-32y-32x^2y+8x=0$
$\Leftrightarrow (8x^3+8x)-(32y+32x^2y)=0$
$\Leftrightarrow 8x(x^2+1)-32y(1+x^2)=0$
$\Leftrightarrow (8x-32y)(x^2+1)=0$
$\Rightarrow 8x-32y=0$ (do $x^2+1>0$ với mọi $x$)
$\Leftrightarrow x=4y$
Khi đó:
$M=\frac{3.4y+2y}{3.4y-2y}=\frac{14y}{10y}=\frac{14}{10}=\frac{7}{5}$