Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Tam giác ABC nhọn:
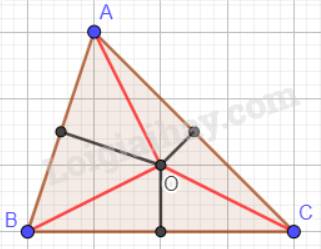
b) Tam giác ABC vuông tại A:
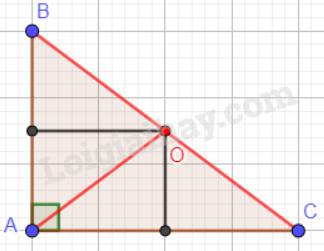
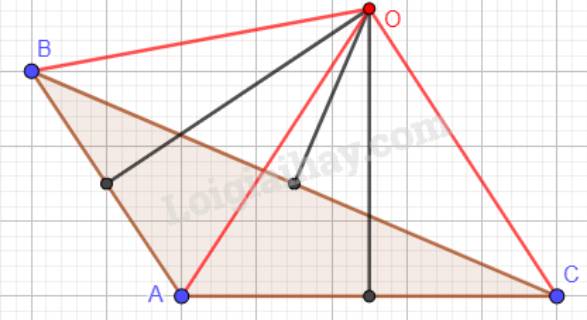
c) Tam giác ABC có góc A tù:

a) \(\widehat{ABC}\) + \(\widehat{BCA}\) = 1800 - \(\widehat{BAC}\) = 1800 - 800 = 1000
Mà theo đề bài \(\widehat{ABC}\) - \(\widehat{BCA}\) = 200
Dùng tổng hiệu => \(\widehat{ABC}\) = 600
\(\widehat{BCA}\) = 400
b) Áp dụng tính chất dãy tỉ số bằng nhau :
\(\frac{\widehat{B}}{11}\) = \(\frac{\widehat{C}}{9}\) = \(\frac{\widehat{B}+\widehat{C}}{11+9}\) = \(\frac{180^0-\widehat{A}}{20}\) = \(\frac{180^0-80^0}{20}\) = 5
=> \(\widehat{B}\)= 550
=> \(\widehat{C}\)= 450

a.
Áp dụng hệ thức lượt trong tam giác vuông ta có:
$\frac{1}{AH^2}=\frac{1}{AB^2}+\frac{1}{AC^2}$
$\Leftrightarrow \frac{1}{AC^2}=\frac{1}{AH^2}-\frac{1}{AB^2}=\frac{1}{3a^2}$
$\Rightarrow AC=\sqrt{3}a$
$BC=\sqrt{AB^2+AC^2}=\sqrt{a^2+3a^2}=2a$
b.
$HB=\frac{BC}{4}$ thì $HC=\frac{3}{4}BC$
$\Rightarrow \frac{HB}{HC}=\frac{1}{3}$
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC; AC^2=CH.BC$
$\Rightarrow \frac{AB}{AC}=\sqrt{\frac{BH}{CH}}=\frac{\sqrt{3}}{3}$
Áp dụng định lý Pitago:
$4a^2=BC^2=AB^2+AC^2=(\frac{\sqrt{3}}{3}.AC)^2+AC^2$
$\Rightarrow AC=\sqrt{3}a$
$\Rightarrow AB=a$
c.
Áp dụng hệ thức lượt trong tam giác vuông:
$AB^2=BH.BC$
$\Leftrightarrow AB^2=BH(BH+CH)$
$\Leftrightarrow a^2=BH(BH+\frac{3}{2}a)$
$\Leftrightarrow BH^2+\frac{3}{2}aBH-a^2=0$
$\Leftrightarrow (BH-\frac{a}{2})(BH+2a)=0$
$\Rightarrow BH=\frac{a}{2}$
$BC=BH+CH=2a$
$AC=\sqrt{BC^2-AB^2}=\sqrt{3}a$
d. Tương tự phần a.

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.
b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.
c)
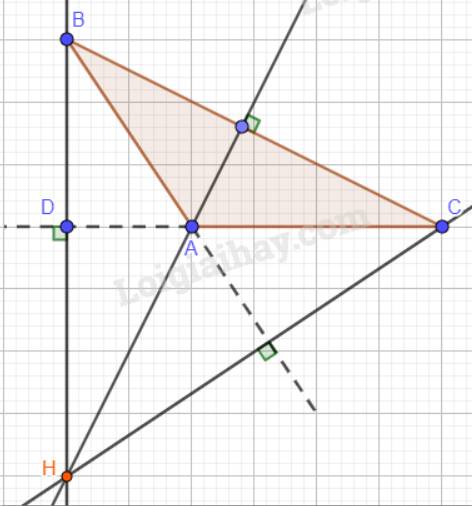
Nhận xét: H nằm ngoài tam giác ABC.

a) Áp dụng công thức: \(S = \frac{1}{2}bc\sin A\), ta có:
\(S = \frac{1}{2}.14.35.\sin {60^o} = \frac{1}{2}.14.35.\frac{{\sqrt 3 }}{2} \approx 212,2\)
Áp dụng đl cosin, ta có: \({a^2} = {b^2} + {c^2} - 2bc.\cos A\)
\(\begin{array}{l}
\Rightarrow {a^2} = {14^2} + {35^2} - 2.14.35.\cos {60^o} = 931\\
\Rightarrow a \approx 30,5
\end{array}\)
\( \Rightarrow R = \frac{a}{{2\sin A}} = \frac{{30,5}}{{2\sin {{60}^o}}} \approx 17,6\)
b) Ta có: \(p = \frac{1}{2}.(4 + 5 + 3) = 6\)
Áp dụng công thức Heron, ta có:
\(S = \sqrt {p(p - a)(p - b)(p - c)} = \sqrt {6(6 - 4)(6 - 5)(6 - 3)} = 6.\)
Lại có: \(S = \frac{{abc}}{{4R}} \Rightarrow R = \frac{{abc}}{{4S}} = \frac{{4.5.3}}{{4.6}} = 2,5.\)

c: Xét ΔABC vuông tại A có
\(AB^2+AC^2=BC^2\)
\(\Leftrightarrow AC=2a\)
Xét ΔABC vuông tại A có
\(\sin\widehat{C}=\dfrac{AB}{BC}=\dfrac{a}{a\sqrt{5}}=\dfrac{\sqrt{5}}{5}\)
\(\cos\widehat{C}=\dfrac{AC}{BC}=\dfrac{2a}{a\sqrt{5}}=\dfrac{2\sqrt{5}}{5}\)
\(\tan\widehat{C}=\dfrac{AB}{AC}=\dfrac{a}{2a}=\dfrac{1}{2}\)
\(\cot\widehat{C}=\dfrac{AC}{AB}=\dfrac{2a}{a}=2\)

c: \(BC=\sqrt{42^2+36^2}=6\sqrt{85}\left(cm\right)\)
\(\widehat{B}\simeq41^0\)
\(\widehat{C}=49^0\)
A+B+C=?
Xét tam giác ABC có : ^A + ^B + ^C = 1800 ( đ.lí )
a) Với ^A/2 = ^B/3 = ^C/4
Áp dụng tính chất dãy tỉ số bằng nhau ta có :
^A/2 = ^B/3 = ^C/4 = ( ^A + ^B + ^C )/( 2 + 3 + 4 ) = 1800/9 = 200
=> ^A = 400 ; ^B = 600 ; ^C = 800
b) Với ^A = ^B = ^C ta có ngay ^A = ^B = ^C = 1800/3 = 600