Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a)

Nhận xét: H là một điểm nằm trong tam giác ABC.
b)

Nhận xét: H trùng với đỉnh A của tam giác ABC.
c)
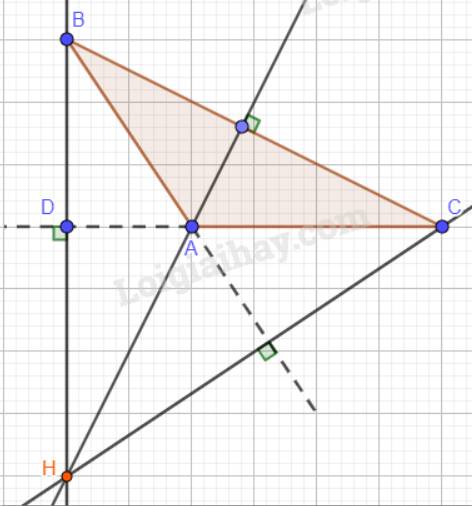
Nhận xét: H nằm ngoài tam giác ABC.

https://h.vn/hoi-dap/tim-kiem?q=Cho+tam+gi%C3%A1c+ABC+c%C3%A2n+t%E1%BA%A1i+A.+K%E1%BA%BB+AH+vu%C3%B4ng+g%C3%B3c+BC+t%E1%BA%A1i+H++a)+CM+tam+gi%C3%A1c+ABH=tam+gi%C3%A1c+ACH++b)+V%E1%BA%BD+trung+tuy%E1%BA%BFn+BM.+G%E1%BB%8Di+G+l%C3%A0+giao+%C4%91i%E1%BB%83m+c%E1%BB%A7a+AH+v%C3%A0+BM.+Ch%E1%BB%A9ng+minh+G+l%C3%A0+tr%E1%BB%8Dng+t%C3%A2m+c%E1%BB%A7a+tam+gi%C3%A1c+ABC++c)+Cho+AB=30cm,+BH=18cm.+T%C3%ADnh+AH,AG++d)+T%E1%BB%AB+H+k%E1%BA%BB+HD+song+song+v%E1%BB%9Bi+AC(D+thu%E1%BB%91c+AB),+ch%E1%BB%A9ng+minh+ba+%C4%91i%E1%BB%83m+C,G,D+th%E1%BA%B3ng+h%C3%A0ng&id=248109

3)- theo bài tao có :A+B+C=180 độ.(định lí tổng ba góc của 1 tam giác)
C:B:A=1:3:6 => C/1=B/3=A/6=(A+B+C)/(1+3+6)=180/10=18
Do đó :C/1=18 B/3=18 A/6=18
=>C=18 độ =>B=54 độ =>A=104 độ
a) Tam giác ABC nhọn:
b) Tam giác ABC vuông tại A:
c) Tam giác ABC có góc A tù: