Cho hình thoi abcd với bd = 35 và tỉ lệ giữa ac và bd là 0.75 Tìm bd
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


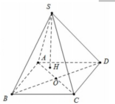
Đáp án C
Ta có: S A O B = 1 4 S A B C D
Do đó V S . A B C D V S . A O B = S A B C D . S H S A O B . S H = 4
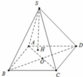

Hình thoi ABCD có hai đường chéo AC và BD cắt nhau tại O (gt)
⇒O là trung điểm của AC và BD
⇒AO=AC2 và DO=BD2
=> AO=6/2=3(cm) và DO = 8/2= 4cm
AC vuông góc BD TẠI O ( vì ABCD là hình thoi )
tam giác ADO vuông góc tại O có AD bình = AO bình + DO bình ( định lý pytago)
=> AD2 =3 bình + 4 bình = 25 => AD= 5cm
Vậy AB=BC=DC=AD=5cm


Do \(ABCD\) là hình thoi nên hai đường chéo vuông góc với nhau tạo ra 4 góc vuông.
Áp dụng ĐL Pythagore vào 1 trong các tam giác vuông, ta có độ dài cạnh hình vuông là:
\(\sqrt {{{\left( {\frac{6}{2}} \right)}^2} + {{\left( {\frac{8}{2}} \right)}^2}} = \sqrt {9 + 16} = \sqrt {25} = 5\) (cm)

Ta có: \(S_{ABCD}=\dfrac{1}{2}.BD.AC\)(với S là diện tích)
\(\Rightarrow\dfrac{1}{2}.2a.8a=32\)
\(\Rightarrow8a^2=32\)
\(\Rightarrow a^2=4\)
\(\Rightarrow a=2\left(cm\right)\)
Bc nhé = 35