Cho (O) đường kính AB. Trên tia đối của tia BA lấy 1 điểm C. Vẽ (C;CO), tiếp tuyến chung của 2 đường tròn tiếp xúc với (O) tại D, tiếp xúc với (C) tại E. Cmr: Khi C di động trên tia đối của BA thì E di động trên 1 đường thẳng cố định.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Xét ΔOBC có OB=OC
nên ΔOBC cân tại O
mà \(\widehat{CBO}=60^0\)
nên ΔOBC đều
Xét ΔOCM có
CB là đường trung tuyến
CB=OM/2
Do đó: ΔOCM vuông tại C
hay MC là tiếp tuyến của (O)

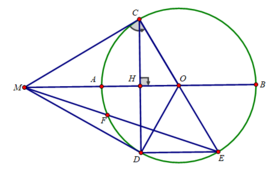
b) Ta có: OM = OA + AM = R + R = 2R
Xét tam giác MCO vuông tại C, CH là đường cao có:
MO 2 = MC 2 + OC 2
![]()
CH.OM = CM.CO
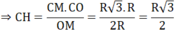
Lại có: CD = 2CH ⇒ CD = R 3
Tam giác CDE nội tiếp (O) có CE là đường kính nên ΔCDE vuông tại D
Theo định lí Py ta go ta có:
CE 2 = CD 2 + DE 2
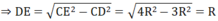

a. Ta có : \(\hat{BDM}=90^o\) (kề bù với \(\hat{BDA}\) nội tiếp chắn nửa đường tròn).
\(\hat{BCM}=90^o\left(gt\right)\)
Vậy : BCMD nội tiếp được một đường tròn (\(\hat{BDM}+\hat{BCM}=180^o\)) (đpcm).
b. Xét △ADB và △ACM :
\(\hat{ADB}=\hat{ACM}=90^o\)
\(\hat{A}\) chung
\(\Rightarrow\Delta ADB\sim\Delta ACM\left(g.g\right)\)
\(\Rightarrow\dfrac{AD}{AC}=\dfrac{AB}{AM}\Leftrightarrow AD.AM=AB.AC\) (đpcm).
c. Ta có : \(OD=OB=BD=R\) ⇒ △ODB đều.
\(\Rightarrow S_{\Delta ODB}=\dfrac{\sqrt{3}}{4}R^2\)
\(\hat{BOD}\) là góc ở tâm chắn cung BD \(\Rightarrow sđ\stackrel\frown{BC}=\hat{BOD}=60^o\) (do △ODB đều).
\(S_{ODB}=\dfrac{\text{π}R^2n}{360}=\dfrac{\text{π}R^2.60}{360}=\dfrac{\text{π}R^2}{6}\)
\(\Rightarrow S_{vp}=S_{ODB}-S_{\Delta ODB}=\dfrac{\text{π}R^2}{6}-\dfrac{\sqrt{3}}{4}R^2\)
\(=\dfrac{\text{π}}{6}R^2-\dfrac{\sqrt{3}}{4}R^2\)
\(=\dfrac{2\text{π}-3\sqrt{3}}{12}R^2\)

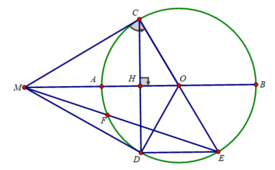
c) Ta có: ΔCOD cân tại O có OH là đường cao cũng là đường trung tuyến của tam giác
⇒ CH = HD = CD/2 ⇒ C H 2 = D H 2 = C D 2 / 4
Tam giác ACH vuông tại H có:
A H 2 + C H 2 = C A 2 ⇒ A H 2 + C D 2 / 4 = C A 2 (1)
Tam giác CHB vuông tại H có:
B H 2 + C H 2 = C B 2 ⇒ B H 2 + C D 2 / 4 = C B 2 (2)
Từ (1) và (2) ta có:
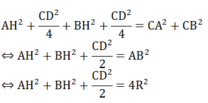

a: Xét (O) có
ΔABC nội tiếp
BC là đường kính
Do đó: ΔABC vuông tại A
ΔABC vuông tại A
=>\(AB^2+AC^2=BC^2\)
=>\(AC^2=10^2-6^2=64\)
=>AC=8(cm)
c: Sửa đề: Chứng minh CB=CD
Xét ΔCBD có
CA là đường cao
CA là đường trung tuyến
Do đó: ΔCBD cân tại C
=>CB=CD

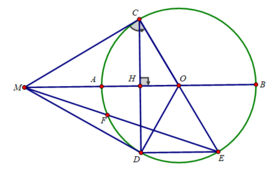
a) Xét tam giác COD cân tại O có OH là đường cao
⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)
Xét ΔMCO và ΔMOD có:
CO = OD
∠(COM) = ∠(MOD)
MO là cạnh chung
⇒ ΔMCO = ΔMOD (c.g.c)
⇒ ∠(MCO) = ∠(MDO)
∠(MCO) = 90 0 nên ∠(MDO) = 90 0
⇒ MD là tiếp tuyến của (O)

a: Điểm M ở đâu vậy bạn?
b: góc ONP=góc ONB+góc PNB
góc ANB=1/2*sđ cung AB=90 độ
=>BN vuông góc AK
=>BN//KC
=>góc ABN=góc ACK
=>góc ONB=góc ACK
Xét ΔKBC có
KP vừa là đường cao, vừa là trung tuyến
=>ΔKBC cân tại K
=>góc BKP=góc CKP
góc ONP=góc ONB+góc BNP
=góc ONB+góc BKP
=góc ONB+góc CKP
=góc OBN+góc NAB=90 độ
=>NP là tiếp tuyến của (O)

b: góc ONP=góc ONB+góc PNB
góc ANB=1/2*sđ cung AB=90 độ
=>BN vuông góc AK
=>BN//KC
=>góc ABN=góc ACK
=>góc ONB=góc ACK
Xét ΔKBC có
KP vừa là đường cao, vừa là trung tuyến
=>ΔKBC cân tại K
=>góc BKP=góc CKP
góc ONP=góc ONB+góc BNP
=góc ONB+góc BKP
=góc ONB+góc CKP
=góc OBN+góc NAB=90 độ
=>NP là tiếp tuyến của (O)
a: KNBP nội tiếp
=>góc PNK=góc PBK; góc PKN=180 độ-góc NBP
=>góc PNK=góc PCK
=>góc PNK=góc AKP
180 độ-góc NBP=góc ABN
=>180 độ-góc NBP=góc AKP
=>góc PNK=góc PKN
=>PK=PN