cho tam giác abc có ba góc nhọn kẻ đường cao BH và đường trung tuyến BM trên tia đối của tia BM lấy điếm D sao cho MD=MB . a) tứ giác ABCD là hình gì ? .
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài này nhiều cách bn nhé, mik lm cách ngắn nhất
Tứ giác có hai đường chéo cắt nhau tại trung điểm mỗi đường là hình bình hành
Vì BM là trung tuyến => MA=MC và MD=MB
=> ABCD là hbh
dễ thôi bạn : xét tứ giác abcd có bm là trung tuyến AC nên AM=AC
mà BM=MD (gt) => tứ giác abcd là hbh ( Hai dường chéo = nhau và giao nhau tại trung điểm mỗi đường )

a: Xét ΔMAB và ΔMCD co
MA=MC
góc AMB=góc CMD
MB=MD
=>ΔMAB=ΔMCD
=>AB=CD và góc MAB=góc MCD
=>AB//CD
=>AC vuông góc DC
b: Xét tứ giac ABCD có
M là trung điểm chung của AC và BD
=>ABCD là hình bình hành
=>AD//BC và AD=BC

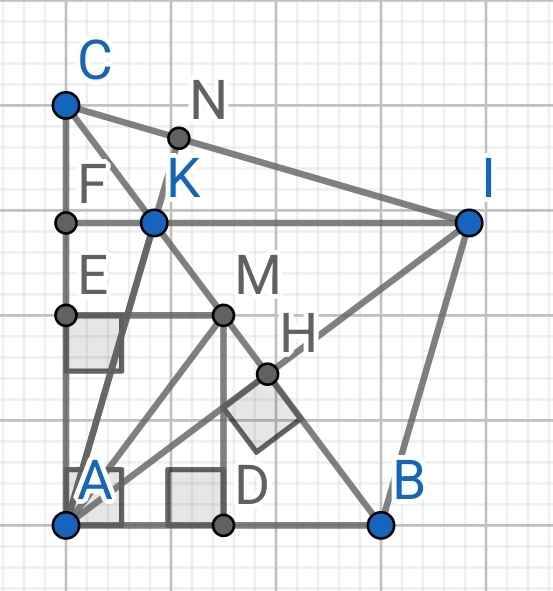
a) Tứ giác ADME có:
∠AEM = ∠ADM = ∠EAD = 90⁰ (gt)
⇒ ADME là hình chữ nhật
b) Do HI = HA (gt)
⇒ H là trung điểm của AI
Do HK = HB (gt)
⇒ H là trung điểm của BK
Tứ giác ABIK có:
H là trung điểm của AI (cmt)
H là trung điểm của BK (cmt)
⇒ ABIK là hình bình hành
⇒ IK // AB
Mà AB ⊥ AC (∆ABC vuông tại A)
⇒ IK ⊥ AC
⇒ IK là đường cao của ∆ACI
Lại có:
AH ⊥ BC (do AH là đường cao của ∆ABC)
⇒ CH ⊥ AI
⇒ CH là đường cao thứ hai của ∆ACI
∆ACI có:
IK là đường cao (cmt)
CH là đường cao (cmt)
⇒ AK là đường cao thứ ba của ∆ACI
⇒ AK ⊥ IC
Đề sai rồi thì phải bạn, mik vẽ nó ra thế đấy =.='
hình đây