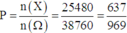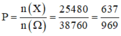Có 2 lô sản phẩm:
Lô 1: có 6 chính phẩm và 4 phế phẩm.
Lô 2: có 4 chính phẩm và 2 phế phẩm.
a, Chọn ngẫu nhiên 1 lô, từ lô đó lấy ngẫu nhiên 2 sản phẩm. Tính xác suất để trong 2 sản phẩm lấy ra có một chính phẩm.
b, Từ lô 1 lấy ngẫu nhiên 2 sản phẩm bỏ vào lô 2, sau đó từ lô 2 lấy ngẫu nhiên ra 1 sản phẩm thấy là chính phẩm. Tính xác suất để sản phẩm lấy ra là từ lô 1 bỏ sang.