giúp em câu 4,5,6 ạ. e gửi ảnh ở phần cmt nha
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bạn kiểm tra lại đề bài câu a, n=1 thì VT=1, VP=-1, nếu đề bài đúng thì vp phải là \(\dfrac{-\left(1\right)^{n-1}n\left(n+1\right)}{2}\)
\(n=1\Rightarrow VT=1=VP\)
Vậy mệnh đề đúng với n=1
Giả sử mệnh đề cũng đúng với \(n=k\left(k\in N\right)\), hay:
\(1^2-2^2+...+\left(-1\right)^{k-1}.k^2=\dfrac{\left(-1\right)^{k-1}.k.\left(k+1\right)}{2}\)
Ta cần chứng minh mệnh đề cũng đúng với \(n=k+1\) ,hay:
\(1^2-2^2+...+\left(-1\right)^{k-1}.k^2+\left(-1\right)^k.\left(k+1\right)^2=\dfrac{\left(-1\right)^k.\left(k+1\right)\left(k+2\right)}{2}\)
That vay:
\(VT=\dfrac{\left(-1\right)^{k-1}k\left(k+1\right)}{2}+\left(-1\right)^k.\left(k+1\right)^2=\dfrac{\left(-1\right)^{k-1}.k.\left(k+1\right)+2\left(-1\right)^k\left(k+1\right)^2}{2}\)
\(=\dfrac{\left(-1\right)^k\left(k+1\right)\left(-k+2k+2\right)}{2}=\dfrac{\left(-1\right)^k\left(k+1\right)\left(k+2\right)}{2}=VP\)
Vậy mệnh đề đúng với \(\forall n\in N\)
b/ \(n=7\Rightarrow VT=3^7=2187< 7!=5040\)
Vậy mệnh đề đúng với n=7
Giả sử mệnh đề đúng với \(n=k\left(k\in N;k\ge7\right)\),hay:
\(3^k\le k!\)
Ta cần chứng minh mệnh đề cũng đúng với \(n=k+1\) ,hay:
\(3^{k+1}\le\left(k+1\right)!\)
That vay:
\(3^k.3\le\left(k+1\right).k!\)
\(k>6\Rightarrow k+1>6\Rightarrow k+1>3\)
Ma \(3^k\le k!\)
\(\Rightarrow3^k.3\le\left(k+1\right).k!\Leftrightarrow3^{k+1}\le\left(k+1\right)!\)
Vậy mệnh đề đúng với \(\forall n\in N;n>6\)


1, \(2x+3x-6x=-x\)
2, \(5x^2+\dfrac{3}{2}x^2-\dfrac{2}{3}x^2=\dfrac{35}{6}x^2\)
3, \(-2x^2y+\dfrac{2}{7}x^2y-3x^2y=-\dfrac{33}{7}x^2y\)
4, \(15x^2y^2+\dfrac{13}{2}x^2y^2-x^2y^2+\dfrac{x^2y^2}{2}=21x^2y^2\)
5, \(-\dfrac{14}{5}x^ny^m-2x^ny^m+2,5x^ny^m=-\dfrac{23}{10}x^ny^m\)
mình thiếu câu 5 :v câu 5 bài trước là câu 6 nhé
\(3x^2y^2z-\dfrac{7}{2}x^2y^2z+\dfrac{1}{2}x^2y^2z=0\)

Để tính quãng đường đi được từ thời điểm t1 đến t2 cho vật giao động điều hòa dọc theo trục Ox, ta cần tính diện tích dưới đường cong x(t) trong khoảng thời gian từ t1 đến t2.
Trước tiên, chúng ta sẽ tính x(t) tại t1 và t2:
Tại t1 = 13/6 s: x(t1) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tại t2 = 23/6 s: x(t2) = 3 * cos(4 * 3.14 - (3.14 / 3)) cm
Tiếp theo, chúng ta cần tính diện tích dưới đường cong trong khoảng từ t1 đến t2. Để làm điều này, ta sẽ tính diện tích của hình giữa đồ thị và trục Ox trong khoảng từ t1 đến t2.
Diện tích A = ∫(t1 đến t2) x(t) dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - (3.14 / 3))] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(4 * 3.14 - 3.14/3)] dt
A = ∫(13/6 đến 23/6) [3 * cos(12.56 - 1.0467)] dt
A = ∫(13/6 đến 23/6) [3 * cos(11.5133)] dt
Giải tích phần này trở nên phức tạp, nhưng bạn có thể tính toán nó bằng máy tính hoặc phần mềm tính toán. Kết quả sẽ là diện tích A, tức là quãng đường đi được từ t1 đến t2.
(em thay pi=3,14 luôn nha anh )




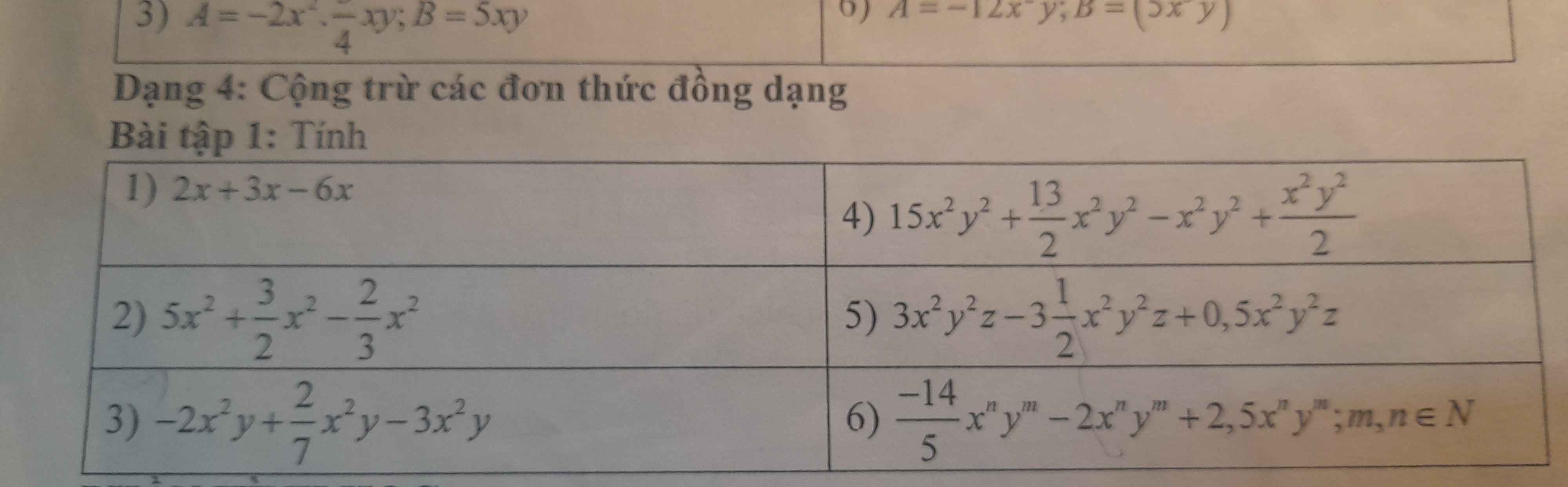

Câu 7:
Trái Đất không tự quay thì vẫn có ngày và đêmCòn khi nó không quay thì hiển nhiên sẽ có một nửa mặt cầu không bao giờ nhận được ánh sáng.
Câu 5:
Sự vận động tự quay quanh trục của Trái Đất
=> Chia bề mặt Trái Đất thành 24 khu vực giờ.
Hệ quả sự vận động tự quay quanh trục của Trái Đất:
a) Hiện tượng ngày, đêm
Khắp mọi nơi trên Trái đất đều lần lượt có ngày và đêm
Diện tích được Mặt Trời chiếu sáng gọi là ngày, diện tích nằm trong bóng tối là đêm.
b) Sự lệch hướng do vận động tự quay quanh trục của Trái Đất
Các vật thể chuyển động trên bề mặt Trái Đất đều bị lệch hướng:
+ Lệch phải ở nửa cầu Bắc
+ Lệch trái ở nửa cầu Nam