Helppppp meeee
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
2
7 tháng 5 2021
a) Vì tam giác ABC cân tại A => \(\widehat{ABC}=\widehat{ACB}=36^o\)
Xét tam giác ABC có:
\(\widehat{ABC}+\widehat{ACB}+\widehat{BAC}=180^o\) (tổng 3 góc của 1 tam giác)
\(\widehat{BAC}=180^o-\left(\widehat{ABC}+\widehat{ACB}\right)\)
\(\widehat{BAC}=180^o-\left(36^o+36^o\right)\)
\(\widehat{BAC}=108^o\)
b, Xét tam giác ABE và tam giác ABF có:
\(\widehat{AEB}=\widehat{AFB}=90^o\)
AB là cạnh chung
\(\widehat{ABE}chung\)
Vậy tam giác ABE = tam giác ABF (ch.gn)
Ý c bạn tự làm nhé
2
7 tháng 5 2021
à thui, mk làm cho lun nè :
Vì ΔABE = ΔABF (câu b)
⇒ \(\widehat{EAB}=\widehat{BFE}\)(hai góc tương ứng) (1)
Xét ΔABF vuông tại F, ta có: \(\widehat{ABF}+\widehat{BAF}\) = 90° (phụ nhau)⇒ \(\widehat{ABF}\) = 90° - \(\widehat{BAF}\) = 90° - 18° = 72° (2)
Từ (3) và (4) suy ra: \(\widehat{EAB}=\widehat{BFE}\left(=72^o\right)\)
Ta có: \(\widehat{EAF}+\widehat{FAD}\) = 180° (kề bù) ⇒ ∠FAD = 180° - \(2\widehat{BAF}\) = 180° - 2. 72° = 180° - 144° = 36° (3)
Xét ΔAFD vuông tại F ta có:
\(\widehat{FAD}+\widehat{FDA}\) = 90° (phụ nhau) ⇒ \(\widehat{FDA}\) = 90° - \(\widehat{FAD}\) = 90° - 36° = 54° (4)
Từ (3) và (4) suy ra:\(\widehat{FDA}>\widehat{FAD}\) ⇒ FA > FD.
Ta có:
AB = AC (ΔABC cân tại A)
AB > BF (định lí: trong tam giác, đường vuông góc là đường ngắn nhất)
⇒ AC > BF
Vì ΔABE = ΔABF (câu b) ⇒ AE = AF (hai cạnh tương ứng)
Mà AF > FD (cmt) ⇒ EA > FD
Vì: BD = BF + FD, EC = EA + AC
Mà: AC > BF (cmt) và EA > FD (cmt)
Vậy: CE > DB
helppppp
helppppp
12 tháng 11 2021
\(\Rightarrow x=\dfrac{5}{12}-\dfrac{1}{4}=\dfrac{1}{6}\)
12 tháng 11 2021
\(0,25+x=\dfrac{5}{12}\Rightarrow\dfrac{1}{4}+x=\dfrac{5}{12}\)
\(\Rightarrow x=\dfrac{5}{12}-\dfrac{1}{4}=\dfrac{5-1.3}{12}=\dfrac{2}{12}=\dfrac{1}{6}\)
20 tháng 2 2022
\(a,\left(2x-1\right)^2-25=0.\\ \Leftrightarrow\left(2x-1\right)^2=25.\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=5.\\2x-1=-5.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=-2.\end{matrix}\right.\)
\(b,\left(x-3\right)\left(5-2x\right)=0.\\ \Leftrightarrow\left[{}\begin{matrix}x-3=0.\\5-2x=0.\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=3.\\x=\dfrac{5}{2}.\end{matrix}\right.\)
\(c,\dfrac{x+1}{x-2}+\dfrac{x-1}{x+2}-\dfrac{2\left(x^2+2\right)}{x^2-4}=0.\)
\(\left(x\ne\pm2\right).\)
\(\Leftrightarrow\dfrac{\left(x+1\right)\left(x+2\right)+\left(x-1\right)\left(x-2\right)-2x^2-4}{\left(x-2\right)\left(x+2\right)}=0.\)
\(\Rightarrow\left(x+1\right)\left(x+2\right)+\left(x-1\right)\left(x-2\right)-2x^2-4=0.\)
\(\Leftrightarrow x^2+3x+2+x^2-3x+2-2x^2-4=0.\)
\(\Leftrightarrow0=0\) (luôn đúng).
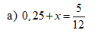
Bạn cần giúp bài nào thì gõ hẳn đề bài đó ra nhé!