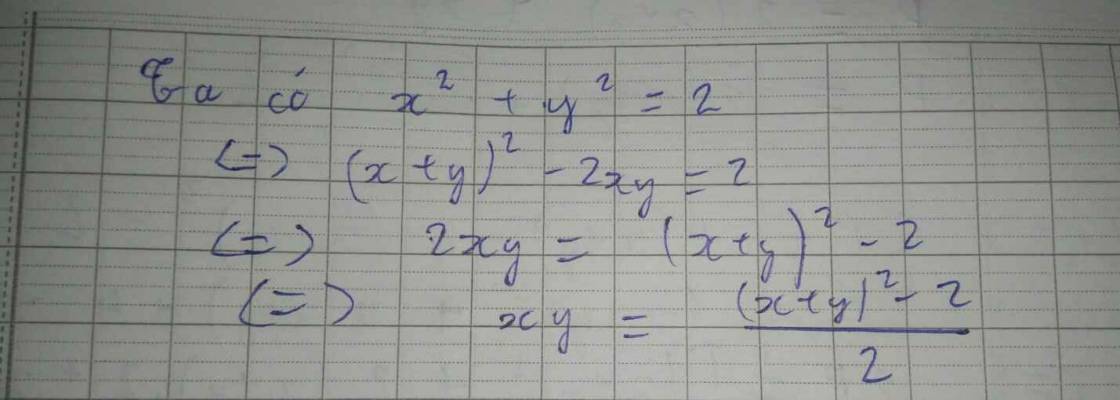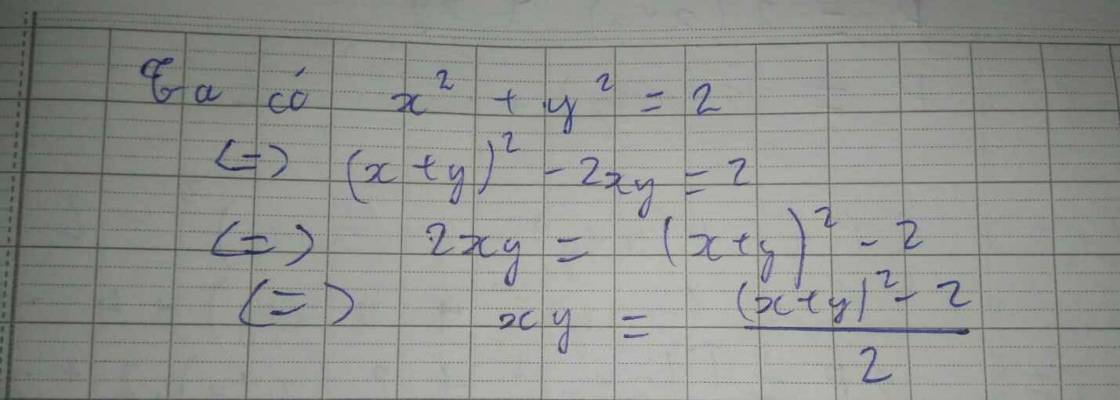Tìm x+y biết (x-2)^2 + x^2 + (y-x)^2 = 2. (x,y là số thực nhé)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
LN
0
2 tháng 12 2021
áp dụng t/c dtsbn ta có:
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{42}{7}=6\)
\(\dfrac{x}{2}=6\Rightarrow x=12\\ \dfrac{y}{5}=6\Rightarrow y=30\)
NV
Nguyễn Việt Lâm
Giáo viên
2 tháng 12 2021
\(\dfrac{x}{2}=\dfrac{y}{5}=\dfrac{x+y}{2+5}=\dfrac{42}{7}=6\)
\(\Rightarrow\left\{{}\begin{matrix}x=2.6=12\\y=5.6=30\end{matrix}\right.\)
16 tháng 1 2021
\(a,x\left(y-2\right)=8\\ \Rightarrow x;\left(y-2\right)\inƯ\left(8\right)=\left\{-8;-4;-2;-1;1;2;4;8\right\}\)
| \(x\) | \(-8\) | \(-4\) | \(-2\) | \(-1\) | \(1\) | \(2\) | \(4\) | \(8\) |
| \(y-2\) | \(-1\) | \(-2\) | \(-4\) | \(-8\) | \(8\) | \(4\) | \(2\) | \(1\) |
| \(y\) | \(1\) | \(0\) | \(-2\) | \(-6\) | \(10\) | \(6\) | \(4\) | \(3\) |
Vậy \(\left(x;y\right)=\left(-8;1\right),\left(-4;0\right),\left(-2;-2\right),\left(-1;-6\right),\left(2;6\right),\left(4;4\right),\left(8;3\right)\)
16 tháng 1 2021
\(b,\left(x-1\right)\left(y-2\right)=9\\ \Rightarrow\left(x-1\right),\left(y-2\right)\inƯ\left(9\right)=\left\{-9;-3;-1;1;3;9\right\}\)
| \(x-1\) | \(-9\) | \(-3\) | \(-1\) | \(1\) | \(3\) | \(9\) |
| \(y-2\) | \(-1\) | \(-3\) | \(-9\) | \(9\) | \(3\) | \(1\) |
| \(x\) | \(-8\) | \(-2\) | \(0\) | \(2\) | \(4\) | \(10\) |
| \(y\) | \(1\) | \(-1\) | \(-7\) | \(11\) | \(5\) | \(3\) |
Vậy \(\left(x;y\right)=\left(-8;1\right),\left(-2;-1\right),\left(0;-7\right),\left(2;11\right),\left(4;5\right),\left(10;3\right)\)
LT
0