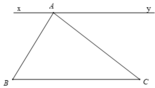
Cho xy//BC.CMR: o. Cái này < là góc.Mình vẽ ko được nhưng nó là hình tam giác có đường thẳng xy đi qua điểm A
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a) Có xy // BC (có hai góc so le trong bằng nhau), mà d // BC nên theo tiên đề Ơ-clit suy ra xy trùng với BC.
b) xy có thể trùng với d hoặc không ( xy trùng với d khi Δ A B C có A B C ^ = A C B ^ )

+ Ta có AB vuông góc với AC và CD vuông góc với AC => AB//CD (cùng vuông góc với AC) (1)
+ Xét tg ABC và tg ACE có
BC=AE
AC chung
BC//AE => ^ACB=^CAE (góc so le trong)
=> tg ABC = tg ACE => ^BAC=^ACE=90 => CE//AB (có 2 góc so le trong bằng nhau) (2)
Từ (1) và (2) => CD trùng CE (qua 1 điểm (điểm C) chỉ dựng được duy nhất 1 đường thẳng // với 1 đường thẳng khác)
=> D; C; E thẳng hàng

a/ Xét tg vuông AOH và tg vuông IOK có
\(OI\perp AH;KI\perp AO\Rightarrow\widehat{KIO}=\widehat{HAO}\)
\(\Rightarrow\Delta AOH\) đồng dạng với \(\Delta IOK\)(Hai tg vuông có hai góc nhọn tương ứng bằng nhau) (1)
b/
Từ (1) \(\Rightarrow\frac{OK}{OH}=\frac{OI}{OA}\Rightarrow OH.OI=OK.OA\)
Ta có \(OA\perp BC\)(Hai tiếp tuyến xuất phát từ 1 điểm ngoài đường tròn thì đường thẳng nối điểm đó với tâm vuông góc và chia đôi dây cung tạo bởi hai tiếp điểm)
Xét tg vuông ABO có \(OB^2=OK.OA=3\) không đổi
\(\Rightarrow OH.OI\)không đổi mà OH không đổi => OI không đổi
Mà H; O cố định => I cố định => Khi A chay trên xy thì BC luôn đi qua điểm I cố định

ta có hình vẽ :
a, Có 6 tam giác đỉnh O là OAB , OAC , OAD , OBC , OBD , OCD
Ta nhận thấy trên đường thẳng xy có bao nhiêu đoạn thẳng thì khi kết hợp với đỉnh O ta được bấy nhiêu tam giác
b, Nếu trên đường thẳng xy có n điểm A1 , A2 , ..., An thì số đoạn thẳng có trên đường thẳng xy là :
\(\frac{n\left(n-1\right)}{2}\)
Do đó số tam giác đỉnh O có hai đỉnh còn lại là 2 trong n điểm A1 , A2 ,..., An là \(\frac{n\left(n-1\right)}{2}\) ( tam giác ).