Vt PT trục đối xứng song song với trục tung của đường tròn (C): x2+y2-2x+3=0
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
18 tháng 9 2017
Đáp án D
(C) có tâm I( 1; – 1), bán kính 1
Đ O y : I => I’( – 1; – 1 )
Phương trình đường tròn (C’): ( x + 1 ) 2 + ( y + 1 ) 2 = 1
CM
21 tháng 10 2019
Đáp án C
(C) có tâm I(0;1) bán kính 2
Đox: I(0;1) -> I’( 0;–1)
Phương trình đường tròn (C’): x 2 + y 2 + 2 y − 3 = 0
CM
15 tháng 5 2019
Đáp án C
(C) có tâm I(1;2) bán kính R = 3
Đ O : I → I’(–1;–2)
Phương trình đường tròn (C’): x + 1 2 + y + 2 2 = 3
CM
30 tháng 11 2017
Gọi M′, d′ và (C') theo thứ tự là ảnh của M, d và (C) qua phép đối xứng qua trục Ox .
Khi đó M′ = (3;5) . Để tìm ta viết biểu thức tọa độ của phép đối xứng qua trục:
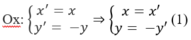
Thay (1) vào phương trình của đường thẳng d ta được 3x′ − 2y′ − 6 = 0.
Từ đó suy ra phương trình của d' là 3x − 2y – 6 = 0
Thay (1) vào phương trình của (C) ta được x ' 2 + y ' 2 − 2 x ′ + 4 y ′ − 4 = 0 .
Từ đó suy ra phương trình của (C') là x − 1 2 + y − 2 2 = 9 .
Cũng có thể nhận xét (C) có tâm là I(1; −2), bán kính bằng 3,
từ đó suy ra tâm I' của (C') có tọa độ (1;2) và phương trình của (C') là x − 1 2 + y − 2 2 = 9
1 tháng 12 2021
\(a,\text{Gọi đt cần tìm là }\left(d\right):y=ax+b\\ \text{Theo đề ta có: }\left\{{}\begin{matrix}a=2;b\ne-3\\\dfrac{1}{3}a+b=\dfrac{4}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=2\\b=\dfrac{2}{3}\end{matrix}\right.\\ \Leftrightarrow\left(d\right):y=2x+\dfrac{2}{3}\\ b,\text{Gọi đt cần tìm là }\left(d'\right):y=ax+b\\ B\left(\dfrac{2}{3};0\right)\text{ và }A\left(0;3\right)\in\left(d'\right)\Leftrightarrow\left\{{}\begin{matrix}\dfrac{2}{3}a+b=0\\b=3\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=-\dfrac{9}{2}\\b=3\end{matrix}\right.\\ \Leftrightarrow\left(d'\right):y=-\dfrac{9}{2}x+3\)
CM
2 tháng 7 2019
Đáp án A
Nhữngphát biểu sai: d; f; i
d) Qua phép đối xứng trục, đoạn thẳng AB biến thành đoạn thẳng song song và bằng nó hoặc là chính nó.
f) Qua phép đối xứng trục Đa, tam giác có một đỉnh nằm trên a sẽ biến thành chính nó ( chỉ trong trường hợp tam giác đều hoặc tam giác cân cóđỉnh nằm trên trục đối xứng)
i) Hình chữ nhật có 2 trục đối xứng
