cho một hệ hai phương trình bậc nhất hai ẩn . tập nghiệm của phương trình thứ nhất trong hệ được biểu diễn bởi đường thẳng ( d 1 ) ; tập nghiệm của phương trình thứ hai trong hệ được biểu diễn bởi đường thẳng ( d 2 ) . hãy ghép mỗi cụm từ ở cột trái dưới đây với một cụm từ nằm ở cột phải để được khẳng định đúng
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
10 tháng 10 2017
Nếu một hệ phương trình bậc nhất hai ẩn có hai nghiệm phân biệt
⇒ Hệ đó có vô số nghiệm.
Vì hệ có hai nghiệm phân biệt nghĩa là hai đường thẳng biểu diễn tập nghiệm của hai phương trình của hệ có hai điểm chung phân biệt, suy ra chúng trùng nhau.
CM
20 tháng 1 2017
Nếu một hệ phương trình bậc nhất hai ẩn có hai nghiệm phân biệt
⇒ Hệ đó có vô số nghiệm.
Vì hệ có hai nghiệm phân biệt nghĩa là hai đường thẳng biểu diễn tập nghiệm của hai phương trình của hệ có hai điểm chung phân biệt, suy ra chúng trùng nhau.
Kiến thức áp dụng
Một hệ phương trình bậc nhất hai ẩn chỉ có thể có nghiệm duy nhất hoặc vô nghiệm hoặc vô số nghiệm.
HQ
Hà Quang Minh
Giáo viên
30 tháng 9 2023
Bước 1: Mở trang Geoebra
Bước 2: Nhập bất phương trình \(x - 2y + 3 \le 0\) vào ô
Và bấm enter, màn hình sẽ hiển thị như hình dưới. Miền nghiệm của bất phương trình \(x - 2y + 3 \le 0\) là miền được tô màu. Đường nét liền biểu thị miền nghiệm chứa các điểm nằm trên đường thẳng \(x - 2y + 3 = 0\).
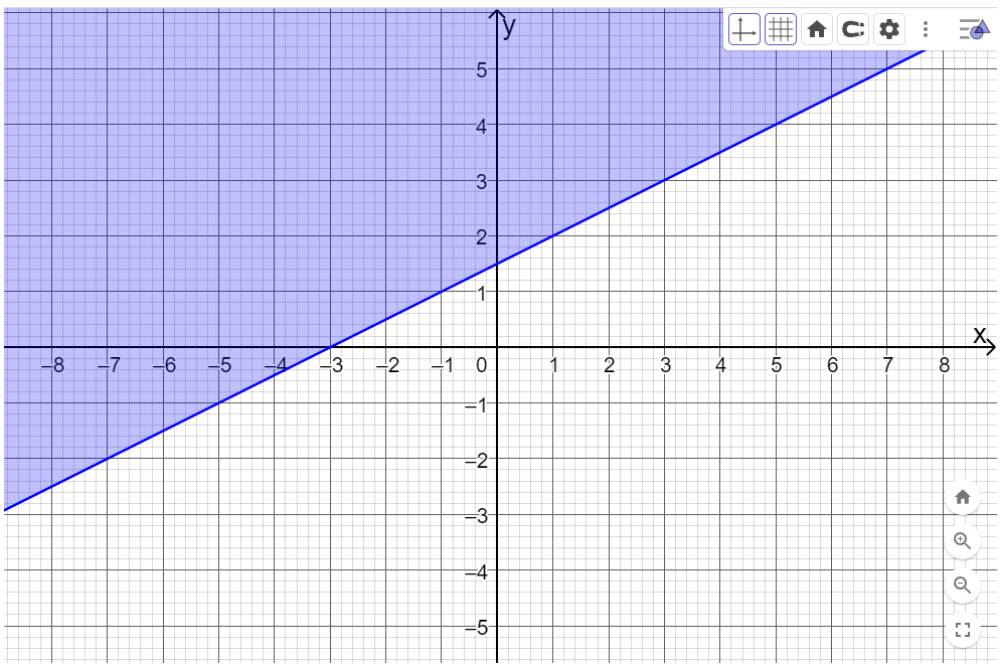
Bước 3: Tiếp tục nhập từng bất phương trình còn lại như sau:
x+3y>-2; \(x \le 0\)(x<=0). Khi đó màn hình sẽ hiển thị như hình dưới.
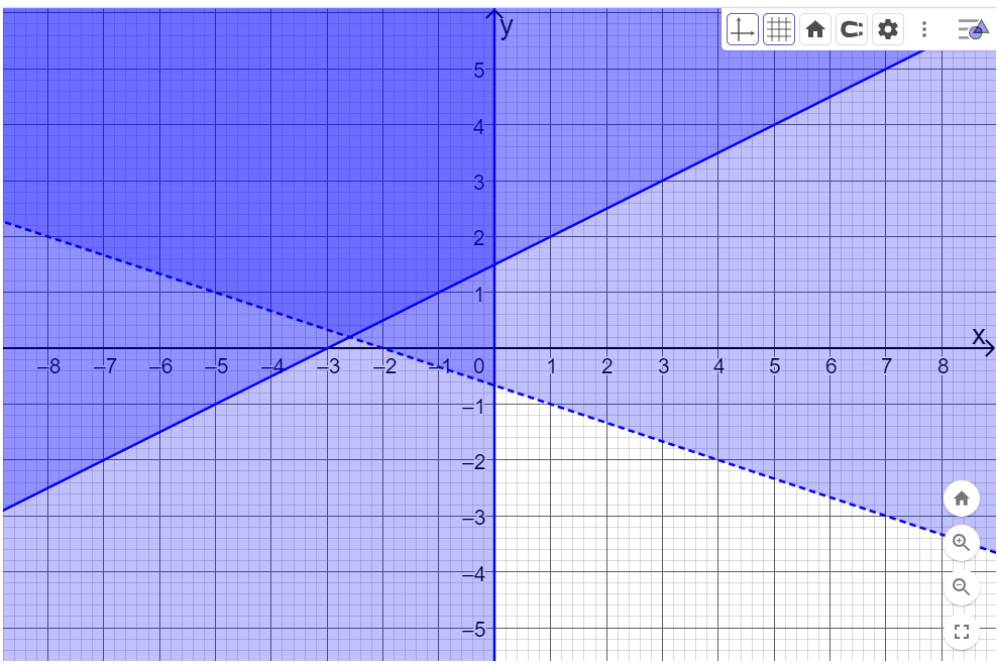
Miền nghiệm của hệ là miền được tô màu đậm nhất. Đường nét đứt biểu thị miền nghiệm không chứa các điểm nằm trên đường thẳng \(x + 3y = - 2\). Đường nét liền \(x = 0\) (trục Oy) biểu thị các điểm nằm trên trục Oy cũng thuộc miền nghiệm.
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 5 2022
(B) hệ đã cho vô nghiệm
vì một phương trình trong hệ đã vô nghiệm
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
23 tháng 5 2022
(B) hệ đã cho vô nghiệm vì một phương trình trong hệ đã vô nghiệm
PT
1
CM
11 tháng 4 2018
Ta biến đổi hệ bất phương trình:
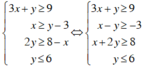
Ta vẽ các đường thẳng 3x + y = 9 (d1); x – y = -3 (d2); x + 2y = 8 (d3); y = 6 (d4)
Nhận thấy (x; y) = (4; 4) thỏa mãn tất cả các bất phương trình của hệ nên A(4; 4) nằm trong miền nghiệm của hệ.
Ta tô đậm các nửa mặt phẳng bờ là các đường thẳng (d1); (d2); (d3); (d4) không chứa điểm A(4 ; 4).
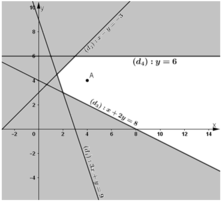
Miền nghiệm của hệ là phần mặt phẳng không bị tô đậm, tính cả các đường biên.
PT
Biểu diễn hình học tập nghiệm của hệ bất phương trình bậc nhất hai ẩn
2 x - y ≤ 3 2 x + 5 ≤ 12 x + 8
1
CM
16 tháng 1 2018
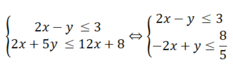
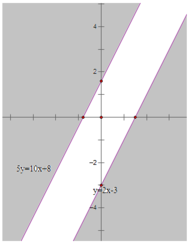
Vẽ các đường thẳng:
(d1): 2x – y = 3 hay y = 2x – 3
(d2): -10x + 5y = 8 hay 5y = 10x + 8
Lấy điểm O(0;0), ta thấy O không thuộc cả 2 đường thẳng trên và 2.0-0 ≤ 3 và - 10.0 + 5.0 ≤ 8 nên phần được giới hạn bởi 2 đường thẳng trên chứa điểm O( phần ko tô đậm) là nghiệm của hệ bất phương trình.
CM
8 tháng 9 2019
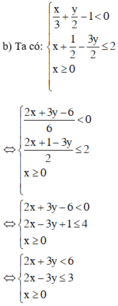
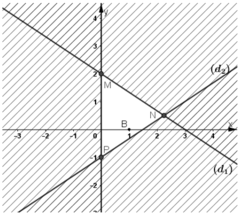
Ta vẽ các đường thẳng 2x + 3y = 6 (d1); 2x – 3y = 3 (d2); x = 0 (trục tung).
Điểm B(1; 0) có tọa độ thỏa mãn tất cả các bất phương trình trong hệ nên ta gạch đi các nửa mặt phẳng bờ (d1); (d2) và trục tung không chứa điểm B.
Miền không bị gạch chéo (tam giác MNP, kể cả cạnh MP và NP, không kể cạnh MN) là miền nghiệm của hệ bất phương trình đã cho.
CM
27 tháng 3 2019
Hệ đã cho vô nghiệm bởi vì mỗi nghiệm của hệ là nghiệm chung của hai phương trình, một phương trình vô nghiệm thì hệ không có nghiệm chung.
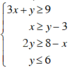
mình đang cần gấp