cho tam giác ABC vuông tại A . Lấy Điểm D bất kỳ thuộc cạnh BC . Gọi E là điểm đối xứng với D qua AB . F là điểm đối xứng với D qua AC
a) Chứng minh E đới xứng với F qua A
b ) Điểm D ở vị trí nào trên cnahj BC thì EF có độ dài ngắn nhất
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
17 tháng 12 2019
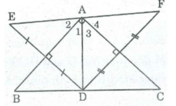
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của ∠ (DAE) ⇒ ∠ A 1 = ∠ A 2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ∆ ADF cân tại A
Suy ra: AC là phân giác của ∠ (DAF)
⇒ ∠ A 3 = ∠ A 4
∠ (EAF) = ∠ EAD) + ∠ (DAF) = ∠ A 1 + ∠ A 2 + ∠ A 3 + ∠ A 4 = 2( ∠ A 1 + ∠ A 3 ) = 2 . 90 0 = 180 0
⇒ E, A, F thẳng hàng có AE = AF = AD
Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.
5 tháng 7 2021
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ∆ ADE cân tại A
Suy ra: AB là đường phân giác của ∠ (DAE) ⇒ ∠ A 1 = ∠ A 2
* Vì F đối xứng với D qua AC
⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ∆ ADF cân tại A
Suy ra: AC là phân giác của ∠ (DAF)
ok!!!!
OF
7 tháng 10 2020
* Vì E đối xứng với D qua AB
⇒ AB là đường trung trực của đoạn thẳng DE
⇒ AD = AE (tính chất đường trung trực)
Nên ΔADE cân tại A
Suy ra: AB là đường phân giác của ∠(DAE) ⇒ ∠A1= ∠A2
* Vì F đối xứng với D qua AC⇒ AC là đường trung trực của đoạn thẳng DF
⇒ AD = AF (tính chất đường trung trực)
Nên ΔADF cân tại A
Suy ra: AC là phân giác của ∠(DAF)
⇒ ∠A3= ∠A4
∠(EAF) = ∠(EAD) + ∠(DAF) = ∠A1+ ∠A2+ ∠A3+ ∠A4= 2(∠A1+ ∠A3) = 2.90o = 180o
⇒ E, A, F thẳng hàng có AE = AF = AD
Nên A là trung điểm của EF hay điểm E đối xứng với điểm F qua điểm A.
13 tháng 1 2022
a: Xét tứ giác AMDN có
\(\widehat{AMD}=\widehat{AND}=\widehat{MAN}=90^0\)
Do đó: AMDN là hình chữ nhật
b: AC=8cm
\(S_{ABC}=\dfrac{AB\cdot AC}{2}=\dfrac{8\cdot6}{2}=24\left(cm^2\right)\)
c: Ta có: D và E đối xứng nhau qua AB
nên AD=AE
=>ΔADE cân tại A
mà AB là đường trung trực
nên AB là tia phân giác của góc DAE(1)
Ta có: D và F đối xứng nhau qua AC
nên AC là đường trung trực của DF
=>AD=AF
=>ΔADF cân tại A
mà AC là đường trung trực của DF
nên AC là tia phân giác của góc DAF(2)
Từ (1) và (2) suy ra \(\widehat{FAE}=2\cdot\left(\widehat{BAD}+\widehat{CAD}\right)=2\cdot90^0=180^0\)
Do đó: F,A,E thẳng hàng
D
3 tháng 8 2021
a/ Nối AM
- Do D đối xứng với M qua AB => AB là đường trung trực của MD
=> AD=AM (t/c đường trung trực)
- Do E đối xứng với M qua AC => AC là đường trung trực của ME
=> AE=AM (t/c đường trung trực)
Từ đó suy ra: AD=AE hay A là trung điểm của DE hay D đối xứng với E qua A (đpcm)
b/ Ta có: AM=AE (cmt)
- Tứ giác MAEC có: AE=AM => Tứ giác MAEC là hình thoi => CE // AM
Tương tự ta cũng có: AM=AD (cmt)
- Tứ giác ADBM có: AM=AD => Tứ giác ADBM là hình thoi => BD // AM
Từ đó suy ra được: BD // CE (đpcm)
c/ Điểm M phải là trung điểm của BC thì DE mới có độ dài nhỏ nhất
9 tháng 9 2016
Võ Hồng Nhung
1 phút trước (15:05)
Cho tam giác ABC. Gọi D, E, F lần lượt là trung điểm của BC, AC, AB. Gọi O là 1 điểm bất kì. A' là điểm đối xứng với O qua D, B' là điểm đối xứng với O qua E, C' là điểm đối xứng với O qua F. Chứng minh AA', BB', CC' đồng quy tại 1 điểm.
a) E đối xứng với D qua AB=> AD=AE và \(\widehat{A_1}=\widehat{A_2}\)
F đối xứng với D qua AC=> AD=AF và \(\widehat{A_3}=\widehat{A_4}\)
\(\Rightarrow AE=\text{AF}\left(=AD\right),\widehat{DAE}+\widehat{D\text{AF}}=2\left(\widehat{A_1}+\widehat{A_3}\right)=2.90^0=180^0\)=> E,A,F thẳng hàng.
Vậy E đối xứng với F qua A(ĐPCM)
b) Ta có: EF=2AD nên EF nhỏ nhất => AD nhỏ nhất => D là chân đường cao kẻ từ A đến BC