Tịnh tiến đồ thị hàm số \(y=-x^2+2\) liên tiếp sang trái 2 đơn vị và xuống dưới 1/2 đơn vị ta được đồ thị của hàm số nào
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Hàm \(y=f\left(x\right)\) có đồ thị (C):
\(\Rightarrow\) Khi tịnh tiến lên a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x\right)+a\)
Khi tịnh tiến xuống dưới a đơn vị ta được đồ thị hàm \(y=f\left(x\right)-a\)
- Khi tịnh tiến sang phải a đơn vị ta sẽ được đồ thị hàm \(y=f\left(x-a\right)\)
- Khi tịnh tiến sang trái a đơn vị sẽ được đồ thị hàm \(y=f\left(x+a\right)\)
Do đó:
Khi tịnh tiến (P) lên 4 đơn vị ta được đồ thị hàm \(y=4x^2+4\)
Khi tịnh tiến (P) sang phải 2 đơn vị ta được đồ thị hàm: \(y=4\left(x-2\right)^2=4x^2-16x+16\)

Chọn D.
Đặt f ( x ) = x 4 - 2 x 2 - 1 thì khi tịnh tiến (C) theo O x qua trái 1 đơn vị thì sẽ được đồ thị của y = f ( x + 1 ) = ( x + 1 ) 4 - 2 ( x + 1 ) 2 - 1 .

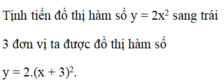


Theo quy tắc dịch đồ thị ta sẽ được hàm \(y=-\left(x+2\right)^2+2-\frac{1}{2}\)
Bạn tự rút gọn