Tìm x,y biết :
3x = y4 và x×y = 12
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
TV
2
MA
1
HA
27 tháng 8 2015
Đề
\(\frac{4}{6\text{x}}-\frac{xy}{6x}=\frac{1}{2}\)
\(\frac{4-xy}{6\text{x}}=\frac{1}{2}\)
8-2xy=6x
4-xy=3x
4=3x+xy
4=x(3+y)
với x=-1 thì 3+y=-4
y=-7
với x=-2thì 3+y=-2
y=-5
với x=-4 thì 3+y=-1
y=-4
với x=1 thì 3+y=4
y=1
với x=2thì 3+y=2
y=-1
với x=4thì 3+y=1
y=-2
NK
1
17 tháng 1 2016
x=-3 ; y=-4 hoặc x=-4; y=-3
các bạn cho mk vài li-ke cho tròn 760 với
5 tháng 8 2019
\(3x=5y\Rightarrow\frac{x}{5}=\frac{y}{3}\)
ÁP DỤNG DÃY TỈ SỐ BẰNG NHAU TA CÓ
\(\frac{x}{5}=\frac{y}{3}=\frac{xy}{15}=\frac{135}{15}=9\)
\(\Rightarrow\hept{\begin{cases}x=45\\y=27\end{cases}}\)
VM
1
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 11 2023
\(\Leftrightarrow x\left(y+5\right)=5y+36\)
\(\Leftrightarrow x=\dfrac{5y+36}{y+5}=\dfrac{5\left(y+5\right)+11}{y+5}=5+\dfrac{11}{y+5}\left(y\ne-5\right)\) (1)
x nguyên khi \(11⋮\left(y+5\right)\)
\(\Rightarrow\left(y+5\right)=\left\{-11;-1;1;11\right\}\)
\(\Rightarrow y=\left\{-16;-6;-4;6\right\}\) Lần lượt thay các giá trị của y vào (1) để tìm các giá trị tương ứng của x
D
0
CM
18 tháng 11 2019
Đặt x2 = a (a ≥ 0), y2 = b (b ≥ 0)
Ta có: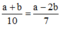 
và a2b2 = 81.
Theo tính chất của dãy tỉ số bằng nhau ta có:
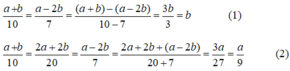
Từ (1) và (2) suy ra a/9 = b ⇒ a = 9b
Do a2b2 = 81 nên (9b)2.b2 = 81 ⇒ 81b4 = 81 ⇒ b4 = 1 ⇒ b = 1 (vì b ≥ 0)
Suy ra a = 9. 1 = 9
Ta có x2 = 9 và y2 = 1. Suy ra x = 3 hoặc x = -3, y = 1 hoặc y = -1.
N
1
3x = 4y => \(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{4}}\)
Đặt \(\frac{x}{\frac{1}{3}}=\frac{y}{\frac{1}{4}}=k\Rightarrow\hept{\begin{cases}x=\frac{1}{3}k\\y=\frac{1}{4}k\end{cases}}\)
xy = 12
<=> \(\frac{1}{3}k\cdot\frac{1}{4}k=12\)
<=> \(\frac{1}{12}k^2=12\)
<=> \(k^2=144\)
<=> \(k=\pm12\)
Với k = 12 => \(\hept{\begin{cases}x=12\cdot\frac{1}{3}=4\\y=12\cdot\frac{1}{4}=3\end{cases}}\)
Với k = -12 => \(\hept{\begin{cases}x=-12\cdot\frac{1}{3}=-4\\y=-12\cdot\frac{1}{4}=-3\end{cases}}\)
Ta có : \(3x=4y\Rightarrow\frac{x}{4}=\frac{y}{3}\)
đặt \(k=\frac{x}{4}=\frac{y}{3}\)
\(\Rightarrow x=4k;y=3k\)
Ta có : \(xy=12\Rightarrow4k.3k=12\)
\(12k^2=12\)
\(k^2=1\)
\(\Rightarrow k=1\)
\(\Rightarrow x=4.1=4\)
\(y=3.1=3\)
Vậy x = 4 ; y = 3