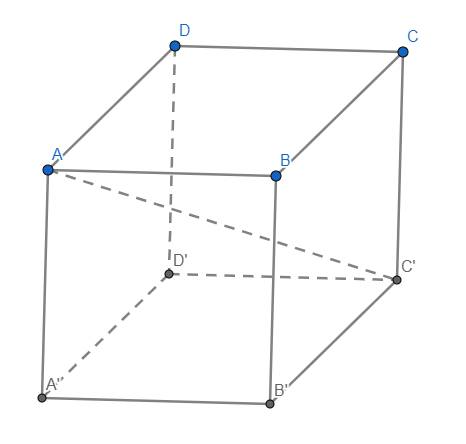
Cho hình lập phương ABCD.A'B'C'D'. M, N, Q lần lượt là trung điểm của BC, C'D', AA'
a) Tìm E = MN giao (ACC'). Chứng minh: E là trung điểm của MN
b) Chứng minh: QE, AC', BD' đồng quy
c) Tìm I = BD' giao (MNQ). Chứng minh: I là trọng tâm tam giác MNQ
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(3AB^2=AC'^2=9a^2\) \(\Leftrightarrow AB^2=3a^2\Leftrightarrow AB=a\sqrt{3}\)
\(\Rightarrow V_{hlp}=AB^3=3a^3\sqrt{3}\) (đơn vị thể tích)

\(\overrightarrow{BD}.\overrightarrow{D'C}=\overrightarrow{BD}\left(\overrightarrow{D'D}+\overrightarrow{DC}\right)=\overrightarrow{BD}.\overrightarrow{D'D}+\overrightarrow{BD}.\overrightarrow{DC}\)
\(=\overrightarrow{BD}.\overrightarrow{DC}=-\overrightarrow{DB}.\overrightarrow{DC}=-a\sqrt{2}.a.cos45^0=-a^2\)

Đáp án C
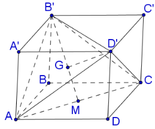
Nhận thấy chóp ACD′B′ có tất cả các
cạnh bằng nhau và bằng 2 2 a
Gọi M là trung điểm của AC, G là
trọng tâm của tam giác AB′C′.
Chóp ACD′B′ nhận D′G là đường cao.
Xét tam giác AB′C′ có


Hướng dẫn:
Gọi P, H lần lượt là trung điểm CD, B'C' \(\Rightarrow\) PMHN là hình chữ nhật
Gọi K, G lần lượt là giao điểm của AC và PM, A'C' là HN \(\Rightarrow\) K, G lần lượt là trung điểm PM và NH
Điểm E chính là giao điểm của MN và KG.
Với việc K, G là trung điểm 2 cạnh đối hcn và MN là đường chéo của hcn thì hiển nhiên E sẽ là trung điểm MN
b.
Do E là trung điểm PG (và MN) nên QE song song AC
Do đó QE, AC', BD' cùng đi qua tâm I của lập phương
c.
Như câu b thì I đồng thời là tâm lập phương
QI đi qua trung điểm E của MN đồng thời \(\frac{QI}{QE}=\frac{AO}{AK}=\frac{2}{3}\) (với O là tâm hình vuông ABCD) nên I là trọng tâm QMN